Введение

Настоящий курс посвящён некоторым аспектам создания изображений и анимации при помощи вычислительных устройств.

Вообще говоря, генерируемые при помощи компьютера изображения можно поделить как минимум на два класса:

• условно «фотореалистичные» — те, для генерации которых требуются значительные вычислительные ресурсы (соответствующие минутам, часам и даже дням вычислений)
• условно «интерактивные» — те, которые можно сгенерировать на доступном оборудовании за доли секунды

Принципы создания изображений и алгоритмы их визуализации для этих классов весьма непохожи друг на друга. Мы будем говорить почти исключительно о втором классе изображений, а содержание этого курса весьма сильно привязано к возможностям графических процессоров второй половины 2010-х (говоря точнее, — к возможностям графических процессоров игровых приставок 8-го поколения).

При этом отдельно отметим, что этот курс посвящён не тому, как при помощи тех или иных программных продуктов получить желаемое изображение, а тем алгоритмам, которые набор входных данных (какие-то числа, представляющие информацию о структуре изображаемого объекта) преобразуют в итоговое изображение.

История

В процессе написания

Инструментарий

Для иллюстрации рассматриваемых алгоритмов мы будем использовать т.н. «веб-технологии» — те средства, которые предоставляют веб-браузеры (которые уже весьма давно из средств отображения гипертекстовых документов превратились в почти полноценные операционные системы).

Язык Javascript

Родным языком программирования (родным в том смысле, в котором таковыми являются разнообразные «ассемблеры» для реальных CPU) для браузеров является Javascript.

Javascript является типичным процедурно-ориентированным скриптовым языком. Его семантика, например, весьма близка таким языкам как Python, PHP, Lua.

Впрочем, у Javascript есть несколько уникальных особенностей, о которых следует упомянуть.

Реактивная модель исполнения

Обычно языки программирования работают по императивной модели: один (или несколько) исполнитель последовательно выполняет команды, из которых состоит программа. Когда команды закончились, программа завершается.

Для Javascript ситуация несколько иная:

• исполнитель всегда ровно один
• но он умеет находиться не только в состоянии исполнения команд, но и в состоянии ожидания
• выводят его из состояния ожидания какие-то внешние события, с которыми связана функция-обработчик
• выйдя из состояния ожидания, исполнитель полностью выполняет функцию-обработчик, не прерываясь и не переходя к исполнению других функций-обработчиков до завершения выполнения текущей функции

По похожей реактивной модели работают центральные процессоры за тем исключением, что в них либо нет никакой «очереди событий», либо же она максимально примитивна и сильно ограничена в размере.

Отсутствие стандартного окружения

В Javascript есть минимальный набор стандартных средств для работы со встроенными в язык типами данных. Весь же набор средств для общения со внешним миров не стандартизирован и определяется конкретной реализацией языка.

Тем не менее, в подавляющем большинстве случаев используется одно из двух «окружений»:

• «браузерное»
• «серверное»

Первое доступно во всевозможных браузерах, и именно с ним мы будем работать (для разных браузеров оно немного разное, но, к счастью, различия не слишком существенны).

Второе — это проект Node.js, позволяющий использовать Javascript как язык для управления ОС.

Не лишним будет сказать о проектах типа Electron, которые совмещают в себе два вышеупомянутых окружения и используются для кроссплатформенных приложений с нетривиальным пользовательским интерфейсом.

Упор на функциональное программирование

Несмотря на то, что Javascript копирует синтаксис языков C, C++, Java и им подобных, а семантикой очень напоминает Python, типичные методологии программирования на нём существенно отличаются от таковых для тех самых C, C++, Java, Python и т.п.

Например, Javascript был одним из первых языков программирования, впитавших монадный подход к асинхронному программированию (пришедший из экосистемы языка Haskell). И вообще изначально задумывался как язык семейства ЛИСП с джаваподобным синтаксисом.

Как следствие, программы на Javascript очень активно используют функции, которые получают на вход другие функции и собирают из них какие-то ещё функции. Более того, в лучших традициях функциональных языков программирования функции в Javascript используются не только как средство изоляции блоков кода, но и как средство модуляризации программы (полноценная стандартизированная поддержка модулей появилась в языке не так давно, и до сих пор многие библиотеки ей не пользуются; кроме того, стандартные модули не являются «объектами первого класса» в отличие от функциональных).

Где почитать подробнее про язык

Рекомендуем два источника:

• MDN — справочник не только по Javascript, но и вообще по всем веб-технологиям
• learn.javascript.ru — неплохой (правда, малость многословный) учебник на русском языке

Также в следующем подразделе дана очень краткая справка по наиболее важным аспектам языка.

Немного о Javascript

Это — очень краткая справка по языку. К тому же, немного устаревшая (она писалась в 2016 году; сейчас я её обновил, но только в совсем неактуальных моментах).

Где взять?

В случае с языком Javascript компилятор долго искать не нужно: в этой роли способен выступать любой достаточно современный браузер. Как и в случае большинства языков программирования, у Javascript есть два режима выполнения: интерактивный построчный и неинтерактивный, исполняющий программу целиком.

В качестве интерактивного режима может выступать Javascript-консоль, находящаяся среди Инструментов Разработчика (Developer Tools) браузера.

Выполнить программу целиком можно одим из следующих способов:

1. Включить внутрь html-документа тег script. Внутри этого тега должна находиться программа на Javascript. Распознавание html для содержимого тега script отключено!

2. Использовать пустой тег script с аттрибутом src=путь_к_файлу. Например, так:

<script src="foobar.js"></script>

Отметим также, что существует популярная альтернатива браузерам как Javascript-платформам — Node.js. Обычно её используют тогда, когда по тем или иным причинам удобно исполнять один и тот же кусок кода как на стороне пользователя, просматривающего веб-страницу, так и на стороне сервера, обслуживающего эту страницу. Впрочем, последнее время Node.js для чего только не используют (в том числе — используют как цель для кросскомпиляции программ на других языках).

Основные характеристики языка

Javascript является слабо динамически типизированным языком. Динамическая типизация означает, что типы проверяются только на этапе выполнения программы, но не на этапе компиляции (более того, переменные в Javascript не имеют типов).

Слабая же типизация означает, что даже выражения, которые не типизируются никаким адекватным образом (например, сумма числа и текста) всё равно вычисляются после неявного преобразование каких-то частей выражения к другому типу.

Отметим, что для тех случаев, когда хочется адекватной системы типов, позволяющей выражать часть инвариантов программы и проверять их на этапе компиляции, существует Typescript — система опциональной строгой статической типизации для Javascript.

Основные синтаксические конструкции

Javascript получил своё название от языка Java, у которого он позаимствовал существенную часть синтаксиса (но не семантики). Язык Java, в свою очередь, синтаксис позаимствовал у C++.

Начнём с объявления переменных. Как ни странно, но это — весьма сложная часть языка. В Javascript есть четыре вида объявления переменных:

foo = 3;       // глобальная переменная
var foo = 4;   // переменная, локальная для функции
let foo = 5;   // переменная, локальная для блока
const foo = 6; // неизменяемая переменная, локальная для блока

Обратите внимание! Объявление глобальной переменной по своему виду совпадает с операцией присваивания. Это — распространённый источник ошибок!

Все var-объявления переменных, где бы они ни находились, переносятся в начало функции, их содержащей. Это поведение более-менее аналогично поведению языка Python в аспекте локальных переменных.

Наконец, let и const — предпочтительный способ объявления переменных. Остальные два существуют только для обратной совместимости с кодом, написанным до 2015 года. Причём настоятельно рекомендуется использовать const везде, кроме тех случаев, когда let необходим.

Функции в Javascript задаются при помощи лямбда-выражений. Например:

const sayHello = (name) => { alert("Hello, " + name); };

Сразу скажем, что обе точки-с-запятой здесь необязательны: при их отсутствии компилятор сам поставит их там, где посчитает нужным. К сожалению, алгоритм расстановки точек-с-запятой довольно примитивен и неотключаем. Это приводит к проблемам вида:

const addNumbers = (x,y) => {
  return   // точка-с-запятой будет поставлена здесь!
    x+y;
};

или же

const something = x => {   // единственный вход можно не брать в скобки
  const foo = 2 
  ( generateFoo(foo) )(x)  // эта строчка является потенциальным продолжением предыдущей
                           // поэтому точка-с-запятой в конце предыдущей строчки поставлена не будет
}

Также допустимы объявления функций вида

function foo(x,y,z) { ... }

Все такие объявления обрабатываются компилятором на этапе чтения программы до её выполнения, поэтому, в частности, корректно работает следующее:

sayHello();  // код может встречаться и вне функций!

function sayHello() { ... }  // функция объявлена после её использования

Управляющие конструкции if, while, for, switch, break, continue, return в Javascript работают почти полностью аналогично соответствующим конструкциям из C. Команда goto отсутствует, зато есть возможность помечать циклы метками и выходить сразу из нескольких циклических уровней:

outer: for (let i = 0; i < 10; i += 1) {
  for (let j = 0; j < 10; j += 1) {
    console.log(i+j);

    if (i > j) { break outer; }
  }
}

Различные виды данных

В первом приближении в Javascript есть 8 «типов» данных: boolean, null, undefined, number, string, object, bigint, symbol.

Тип boolean содержит два значения: true и false. Тем не менее, любой объект может быть преобразован к этому типу. Ложными считаются: false, число 0, число -0, число NaN, null, undefined, пустой текст. Всё остальное считается истинным.

Типы null и undefined содержат по одному (одноимённому) значению. Различие между ними следующее: предполагается, что null — вполне корректное значение, которое программист может использовать в своих целях, а undefined — обычно признак ошибки в коде. Впрочем, иногда у них есть и другие назначения. Например, при преобразовании объектов в формат JSON поля со значением null остаются, а со значением undefined — нет.

Числа в Javascript обычно имеют тип number — аналог double из языка C. А именно, это — числа с плавающей точкой двойной точности. В связи с этим с ними нужно соблюдать осторожность: арифметика с плавающей точкой порой значительно отличается по поведению от арифметики целых чисел.

Есть ещё тип bigint. Литералы этого типа имеют суффикс n. Например, 123n. Это — целые числа произвольного размера. Аналогичны целым числам в Python.

Тексты типа string представляют собой неизменяемые массивы символов в кодировке UTF-16 (это означает, что некоторые символы занимают по два «места»). К отдельным символам можно обращаться при помощи квадратных скобок или же метода charAt (например "foobar".charAt(2)). Длина текста хранится в поле length ("foobar".length равно 6). Текстовые литералы можно обозначать как одинарными, так и двойными кавычками — разницы между ними нет. Также есть обратные кавычки, внутри которых:

• можно переходить на новую строчки — ошибки компиляции не будет
• можно вставить текстовое представление значения любой формулы — эту формулу нужно взять в доллар с парой фигурных скобок: ${формула}

Текст можно преобразовать в число функциями parseInt, parseFloat и BigInt.

Тип symbol используется не слишком часто, поэтому мы не будем на нём отдельно останавливаться.

Всё остальное (в том числе функции и массивы) считаются представителями типа object. Поскольку объекты бывают изменяемыми, очень важно понимать семантику операции присваивания. В Javascript присваивание даёт объекту новое имя (в точности как в Python):

a = [1,2,3];
b = a;
b[1] = 4;  // теперь a[1] -- тоже 4, поскольку b и a именуют один и тот же массив

Объекты представляют собой наборы пар ключ-значение, где ключ — произвольный текст, а значение — произвольная единица данных. Литералы объектов оформляются фигурными скобками, ключи и значения разделяются двоеточиями, а пары ключ-значение — запятыми.

Например, так:

const someObject = {
  foo: {  // ключи не обязательно брать в кавычки
    bar: 123, 
    baz: 456 
  },
  "quuz": 789,
};

Получить доступ к полям такого объекта можно как при помощи квадратных скобок (например, someObject["foo"]), так и при помощи точки (например, someObject.foo). Квадратные скобки более универсальны (работают, например, для ключей, состоящих из цифр), но никак не обрабатываются различными оптимизаторами и минификаторами кода (впрочем, оптимизаторы и минификаторы не являются частью языка, да и используются зачастую только для того, чтобы убрать из кода все пробелы и комментарии).

В заключение пара слов о массивах. Массивы ведут себя так, как будто они являются объектами с ключами "0", "1", "2" и так далее.

Тем не менее, для них есть специальная поддержка со стороны языка. Литералы массивов выделяются с двух сторон квадратными скобками. Длина массива хранится в поле length. Доступ к элементам осуществляется при помощи квадратных скобок. Наиболее простой способ скопировать массив: воспользоваться методом slice (foobar.slice() создаёт копию массива, именуемого переменной foobar).

Метод push позволяет добавить элементы в конец массива (например, foobar.push(1,2,3) добавляет элементы 1, 2, 3 в конец массива, именуемого foobar). Можно добавлять элементы и просто при помощи квадратных скобок и присваивания:

foobar[foobar.length] = 1;
foobar[foobar.length] = 2;
foobar[foobar.length] = 3;
// эквивалентно foobar.push(1,2,3)

Циклы «foreach»

Кроме сиподобного цикла for в Javascript есть более лакончиные

• for (let/const переменная in формула)
• for (let/const переменная of формула)

Оба они работают примерно как for из Python: сначала вычисляется значение формулы, а затем, если это значение имеет тип object:

• for in проходится по всем ключам объекта (кроме тех, которые помечены как «неперечисляемые»)
• for of запускает специальный механизм итерации (для произвольно взятого объекта этот механизм не определён; зато определён, например, для массивов, для которых for of в основном и используется)

Сравнение объектов

Отдельный раздел мы посвятим операторам сравнения == и === (и их отрицаниям != и !==). Различие между ними простое: === проверяет только равенство внутри одного типа; объекты разного типа он считает разными; == дополнительно производит преобразование типов. Поскольку запомнить семантику оператора == весьма сложно, не рекомендуется его использовать кроме как для сравнения чисел с текстами, состоящими из цифр. Поэтому мы опишем только действие ===.

• булевы значения сравниваются естественным образом
• null равно null, то же самое — с undefined
• тексты сравниваются посимвольно
• числа сравниваются в соответствии с правилами арифметики с плавающей точкой
• объекты равны только при равенстве указателей (т.е. когда это физически один и тот же объект в памяти компьютера); в частности, обычно [1,2,3] не равен [1,2,3]!

Оператор typeof

В Javascript есть оператор typeof, который позволяет узнать тип объекта. У него есть две особенности:

• typeof null === 'object', несмотря на то, что настоящий тип null называется null
• typeof функция === 'function', хотя функции имеют тип object

Впрочем, обычно typeof используется для того, чтобы отличить текст от числа.

JSON

Javascript породил такой текстовый формат представления данных как JSON. Каждая единица данных в JSON — это одно из:

• число (оформляется стандартным образом)
• текст (оформляется при помощи двойных кавычек)
• список (оформляется при помощи квадратных скобок и запятых)
• объект (оформляется при помощи фигурных скобок и запятых; запятые разделяют пары ключ : значение, где ключ — это текст, а значение — произвольный JSON)
• булево значение: false или true
• значение null

Сам Javascript поддерживает в качестве литералов некоторое надмножество JSON.

Например, объект, соответствующий JSON

{ "foo" : "bar", "baz": { "quuz": 42 } }

в Javascript можно записать как

{ foo: `bar`, baz: { quuz: 42, }, }

Для преобразования между Javascript-объектами и JSON существуют функции JSON.parse (из JSON в JS) и JSON.stringify (из JS в JSON).

Зачастую JSON.stringify — наиболее простой способ сравнить между собой сложные объекты (например, два массива). К сожалению, числа типа bigint не поддерживаются этой функцией.

Функции как замыкания

Если функция объявляется в контексте каких-то переменных и их использует, то эти переменные остаются живы всё то время, пока жива эта функция.

Например, работает следующий код:

function makeAdder(toAdd) {
  return x => toAdd + x;  // тело вида { return формула; } можно заменить просто на эту формулу
}

const foo = makeAdder(3);

console.log(foo(1));  // печатает 4
console.log(foo(2));  // печатает 5

Более того, подобным образом можно сделать «объект» с изменяемым состоянием:

function makeVar(init) {
  let myVar = init;

  return [
    () => myVar,
    (newVal) => { myVar = newVal },
  ];
}

const [ getFoo, setFoo ] = makeVar(42);
console.log(getFoo());  // 42
setFoo(24);
console.log(getFoo());  // 24

И даже — «модуль первого класса»:

function makeLibrary(/*какие-то параметры*/) {

const FOO = /*...*/;
const BAR = /*...*/;

function someFunc1(/*...*/) { /*...*/ }
function someFunc2(/*...*/) { /*...*/ }
function someFunc3(/*...*/) { /*...*/ }

return { someFunc1, someFunc2, someFunc3 };
}

Можно для каждого набора параметров создать свой экземпляр «библиотеки» и одновременно пользоваться несколькими такими экземплярами. Иногда это бывает очень удобно!

Демонстрация

Сейчас мы покажем средства работы с графикой, предоставляемые браузерным окружением.

Полный код примера доступен по ссылке.

Простейший растровый редактор

Мы реализуем растровый редактор: программу, позволяющую редактировать изображение путём изменения цветов его пикселей.

Точка входа: HTML-страница

Основной режим работы браузера: просмотр файлов, написанных на языке HTML. Эти файлы описывают общую структуру «документа» (этим словом называется то, что браузер в итоге рисует).

Также в HTML-файле могут содержаться части, написанные на языке CSS (задают по большей части внешний вид тех или иных компонент документа), и части, написанные на языке Javascript (описывают поведение документа в ответ на действия пользователя или же иные «события»).

Нам сейчас (и далее) не будут требоваться никакие особенности HTML и CSS, поэтому ограничимся самым минимумом:

<!doctype html>

<meta charset="utf8">

<title>Микропэйнт</title>

<script src="main.js"></script>

<canvas id="CANVAS"></canvas>

Этот текст нужно сохранить в какой-нибудь текстовый файл. Желательно, чтобы название файла оканчивалось на .html, а текст кодировался при помощи utf8.

Первая строчка задаёт версию языка HTML.

Вторая — указывает кодировку файла.

Третья — название, которое браузер печатает на соответствующей вкладке. Можно её и не писать.

Четвёртая — указывает, что нужно запустить программу, которая содержится в файле main.js. Хотя HTML позволяет писать Javascript-код между открывающим «тегом» <script> и закрывающим </script>, лучше всё же этот код писать в отдельном файле. И Вам будет проще, и текстовому редактору, которым Вы пользуетесь.

Пятая строчка описывает единственную компоненту документа — элемент canvas. Этот элемент предоставляет различные способы рисовать на нём изображение при помощи программы. «Атрибут» id="CANVAS" задаёт идентификатор элемента: именно по этому идентификатору мы получим доступ к элементу внутри программы.

Событие load

Вообще говоря, Javascript обычно исполняется в ответ на те или иные события. А именно, считав программу из файла, браузер сперва выполняет весь код, находящийся вне определения функций, а затем переходит в режим ожидания.

Режим ожидания прерывается только если происходит что-то. Если при этом к этому чему-то была привязаны какие-то функции, эти функции выполняются друг за другом. При этом выполнение какой-либо из этих функций не может быть прервано другим событием (событие откладывается в очередь, откуда затем достаётся браузером в подходящий момент).

Одним из возможных событий является load. Оно происходит в тот момент, когда браузер заканчивает формирование документа. После этого события из документа можно получить доступ к любому элементу, описанному в HTML.

Функцию-обработчик этого события можно задавать путём изменения глобальной переменной onload (есть также метод .addEventListener, при помощи которого можно задать несколько обработчиков одному и тому же событию, но его использование чревато трудноуловимыми ошибками и, по-хорошему, требует организации системы регистрации обработчиков событий).

Начнём с простого:

onload = () => {
    const canvas = document.getElementById("CANVAS");
    const ctx = canvas.getContext("2d"); 

    ctx.fillStyle = 'red';
    ctx.fillRect(0, 0, ctx.canvas.width, ctx.canvas.height);
}

Первая строчка функции получает элемент с идентификатором CANVAS.

Вторая — получает от этого элемента «контекст» 2d. Под термином «контекст» понимается набор функций для работы с холстом и некоторое внутреннее состояние, обеспечивающее взаимное влияние этих функций друг на друга.

Кроме контекста 2d холст предоставляет ещё контексты webgl и webgl2, которые используются для управления GPU в соответствии со стандартом OpenGL ES.

Описание контекста 2d можно посмотреть, например, на MDN.

Далее демонстрируется метод .fillRect, рисующий сплошной прямоугольник. Управляется поведение этого метода полем .fillStyle, которое позволяет задать цвет прямоугольника. Цвет можно задавать одним из следующих способов:

• названием
• в 16-ричной системе счисления по маске #RGB (например, #a0e)
• в 16-ричной системе счисления по маске #RGBA (например, #a0ef)
• в 16-ричной системе счисления по маске #RRGGBB (например, #aa00ee)
• в 16-ричной системе счисления по маске #RRGGBBAA (например, #aa00eeff)
• в десятичной системе счисления rgb(170,0,238) или rgba(170,0,238,1.0)
• ещё несколькими способами

Отметим, что альфа-канал используется для линейной интерполяции между старым и новым цветами по формуле (для каждой из RGB-компонент)

\[\alpha x + (1-\alpha) X\]

где \(x\) — старое значение компоненты, а \(X\) — новое. Это — самый частый, но далеко не единственный способ использования альфа-канала.

Также отметим, что ctx.canvas.width и ctx.canvas.height можно было бы заменить на просто canvas.width и canvas.height, но более длинным кодом мы продемонстрировали, что холст тоже является частью контекста (и его не обязательно передавать в другие функции, которые рисуют что-то, для чего требуется знать параметры холста).

Реакция на мышь

В конце обработчика допишем пару вспомогательных функций и ещё один обработчик.

    const drawAt = (x, y) => {
        ctx.fillStyle = 'white';
        ctx.fillRect(x - 5, y - 5, 11, 11);
    };

    const getMouseCoords = (data) => {
        const { x, y } = canvas.getBoundingClientRect();

        const curX = data.clientX - x;
        const curY = data.clientY - y;

        return [curX, curY];
    };
    
    canvas.onmousedown = (data) => {
        if (data.button != 0) { return; }

        const [x, y] = getMouseCoords(data);
        drawAt(x, y);
    };

Первая из функций ставит белый квадратик с центром в заданной точке.

Вторая же используется для получения координат указателя мыши по информации, предоставляемой браузером обработчику событий, связанных с мышью (к сожалению, браузер не предоставляет координаты мыши относительно элемента, принявшего событие; поэтому их приходится пересчитывать из глобальных координат).

Теперь мы можем ставить на холст отдельные квадратики.

Рисование линий

Наконец, модифицируем код так, чтобы можно было рисовать непрерывные линии. Первый шаг: добавление переменной, хранящей состояние кнопки мыши (нажата/отжата), и переменных, хранящих предыдущие координаты мыши:

    let buttonPressed = false;
    let prevX = null;
    let prevY = null;

    onmousemove = (data) => {
        if (!buttonPressed) { return; }

        const [curX, curY] = getMouseCoords(data);

        /* рисуем линию между prevX,prevY и curX,curY */

        prevX = curX;
        prevY = curY;
    };

    canvas.onmousedown = (data) => {
        if (data.button != 0) { return; }
        buttonPressed = true;

        const [x, y] = getMouseCoords(data);
        drawAt(x, y);
    };

    onmouseup = (data) => {
        if (data.button != 0) { return; }
        buttonPressed = false;
        prevX = null;
        prevY = null;
    };

Предыдущий canvas.onmousedown нужно заменить на вышеприведённый: в нём есть одна дополнительная строчка buttonPressed = true;.

Отметим, что onmouseup у нас глобальный, а не от холста: мы можем вывести курсор за предел холста и там отпустить кнопку.

Рисование линии можно реализовать, например, одной из модификаций алгоритма Брезенхема:

        if (prevX === null) {
            drawAt(curX, curY);
        } else {
            const dx = curX - prevX;
            const dy = curY - prevY;

            if (dx === 0 && dy === 0) { 
                drawAt(curX, curY);
            } else if (Math.abs(dy) > Math.abs(dx)) {
                for (let i = 0; i <= Math.abs(dy); i++) {
                    const rx = prevX + dx * i / Math.abs(dy); 
                    const ry = prevY + dy * i / Math.abs(dy); 
                    drawAt(rx, ry);
                }
            } else if (Math.abs(dx) >= Math.abs(dy)) {
                for (let i = 0; i <= Math.abs(dx); i++) {
                    const rx = prevX + dx * i / Math.abs(dx); 
                    const ry = prevY + dy * i / Math.abs(dx); 
                    drawAt(rx, ry);
                }
            }
        }

Двумерная графика

Для начала мы рассмотрим некоторые математические аспекты и алгоритмы двумерной графики.

А именно, поговорим о:

• том, как моделировать точки и преобразования множеств точек числами
• том, как строить геометрию, с которой удобно общаться программным образом (наборы отрезков/треугольников), по альтернативным представлениям (облака точек и скалярные поля)

Векторы и линейные преобразования

В компьютерной графике мы изображаем какие-то области плоскости/пространства — сущностей, которые присутствуют только у нас в голове (и, с некоторыми оговорками, — вокруг нас). Компьютер же умеет работать только с числами (да и тоже — с большим количеством оговорок).

Соответственно, первостепенная задача — определиться со способом моделирования плоскости/пространства при помощи чисел.

Пока мы будем говорить лишь о плоскости, но все приведённые рассуждения с минимальными изменениями переносятся на случай пространства.

Системы координат

Если мы фиксируем невырожденный треугольник \(ABC\) (слово «невырожденный» означает, что вершины этого треугольника не лежат на одной прямой), то тогда для любой точки \(X\), зная расстояния \(XA\), \(XB\), \(XC\), можно однозначно восстановить её положение:

• точка \(X\) лежит на окружности с центром в \(A\) и радиусом \(XA\)
• эта же точка лежит на окружности с центром в \(B\) и радиусом \(XB\)
• есть не более двух точек пересечения этих окружностей
• эти точки (в том случае, когда их две) находятся на разном расстоянии от точки \(C\), поэтому ровно одна из них находится на расстоянии \(XC\)

Поэтому любую точку можно задать тремя числами — расстояниями до вершин треугольника. К сожалению, этот подход имеет много недостатков. В частности, такие:

• не все тройки чисел соответствуют точкам
• простейшие геометрические объекты (например, прямая и окружность) имеют очень сложные выражения в терминах таких троек чисел

Тем не менее, сам факт о возможности восстановления положения точки по тройке расстояний, очень полезен и неоднократно понадобится нам в дальнейшем.

А сейчас мы предложим другой подход, который обычно и используется. Проведём из точки \(X\) прямые, параллельные \(AC\) и \(AB\). Первая прямая где-то пересекает прямую \(AB\), вторая — \(AC\). Точки пересечения этих прямых с \(AB\) и \(AC\) назовём \(Y\) и \(Z\) соответственно.

Первой координатой точки \(X\) мы назовём отношение \(AY/AB\) если точка \(Y\) лежит по ту же сторону от \(A\), что и \(B\), и \(-AY/AB\) — в противном случае. Аналогично определим вторую координату точки \(X\) (взяв \(C\) вместо \(B\) и \(Z\) вместо \(Y\)).

Таким образом мы сопоставили каждой точке пару чисел. Более того, любая пара чисел оказалась сопоставлена какой-то одной точке. Самое главное, что теперь любая прямая может быть задана линейным неоднородным уравнением: а именно, прямая — это множество всевозможных точек с координатами \(x_1,x_2\), удовлетворяющими уравнению

\[ ax_1 + bx_2 + c = 0 \]

для какой-то тройки \(a, b, c\), в которой кто-то из \(a\) или \(b\) не ноль.

Более того, если выбрать треугольник \(ABC\) так, что \(\angle BAC = 90^\circ\), а \(AB=AC=1\), то появляются ещё две важные формулы:

• расстояние между точками с координатами \((a_1, a_2)\) и \((b_1, b_2)\) равно \(\sqrt{(a_1-b_1)^2 + (a_2-b_2)^2}\)
• окружность с центром в точке \((a_1, a_2)\) и радиусом \(R\) может быть задана уравнением \((x_1-a_1)^2 + (x_2-a_2)^2 = R^2\)

Векторы

Для практических целей точки не являются слишком удобными объектами: хотя над ними и есть некоторое количество полезных и нетрудно описываемых в вышеприведённой модели операций (например, провести прямую через две точки), формулы, использующие лишь координаты точек, быстро становятся слишком сложными, и поэтому хочется чего-то большего.

И это что-то большее есть — векторы. Самая трудная часть векторов — их определение. Вообще говоря, в математике слово «вектор» употребляется в двух смыслах: «широком» и «узком».

В широком смысле вектор — тип объектов, для которых определены операции:

• сложения двух векторов
• растяжения вектора (в некоторое число раз)

Для этих операций требуется некоторый естественный набор свойств (например, растянуть сумму векторов всё равно что растянуть в такое же число раз каждый из векторов, а затем результаты сложить). В программировании такое называется «интерфейсом» или «абстрактным типом данных».

В узком же смысле вектор — это конкретная геометрическая реализация вышеописанного интерфейса. Причём, есть несколько широкораспространённых подходов. Каждый из них опишем на псевдопитоне.

Подход №1: направленный отрезок с нетрадиционным равенством

class Vector:
    # модель -- пара точек
    def __init__(self, A, B):
        self.src = A
        self.dst = B

    def __eq__(self, other):
        # пусть distance считает расстояние между точками:
        c1 = distance(self.src, self.dst) == distance(other.src, other.dst)

        # пусть same_side(A,B,C,D) определяет, лежат ли C и D по одну 
        # сторону от прямой AB на плоскости, если A!=B,
        # или точки A на прямой AC, если A=B
        c2 = same_side(self.src, other.src, self.dst, other.dst)

        return (c1 and c2)

    def __add__(self, other):
        A = self.src
        B = self.dst
        C = find_sum(B, other) # такая точка, что Vector(B, C) == other
        return Vector(A, C)

    def scale(self, k):
        A = self.src
        B = self.dst

        C = find_scaled(A, B, k) # такая точка, что AC = |k| AB, причём
                                 # B и C по одну или разные стороны от A
                                 # в зависимости от знака k
        return Vector(A, C)

Подход №2: множество направленных отрезков

class Vector:
    def __init__(self, A, B):
        self.names = { 
            (X, Y) 
            for X in plane 
            for Y in plane
            if distance(A, B) == distance(X, Y)
            if same_side(A, X, B, Y)
        }

    def __eq__(self, other):
        return self.names == other.names

    def __add__(self, other):
        for a, b in self.names:
            A, B = a, b
            break

        # пусть extract_wth_src(s, x) выдаёт элемент e множества s, 
        # которого e[0] == x
        _, C = extract_with_src(other.names, B)

        return Vector(A, C)

    def scale(self, k):
        for a, b in self.names:
            A, B = a, b
            break

        C = find_scaled(A, B, k) 
        return Vector(A, C)

Подход №3: пара чисел

Этот подход предполагает, что у каждой точки есть координаты .x и .y в некоторой заранее фиксированной системе координат.

class Vector:
    def __init__(self, A = None, B = None):
        if A == None: 
            self.x = 0
            self.y = 0
        else:
            self.x = B.x - A.x
            self.y = B.y - A.y

    def __eq__(self, other):
        return self.x == other.x and self.y == other.y

    def __add__(self, other):
        result = Vector()
        result.x = self.x + other.x
        result.y = self.y + other.y
        return result
    
    def scale(self, k):
        result = Vector()
        result.x = self.x * k
        result.y = self.y * k
        return result

Подход №4: «закреплённые» вектора

Этот подход предполагает, что есть заранее фиксированная точка P.

class Vector:
    def __init__(self, A, B):
        self.dst = find_end(P, A, B)
        # такая точка Q, что PQ = AB и выполнено same_side(P, A, Q, B)

    def __eq__(self, other):
        return self.dst == other.dst

    def __add__(self, other):
        Q = find_end(self.dst, P, other.dst)
        return Vector(P, Q)

    def scale(self, k):
        Q = find_scaled(P, self.dst, k) 
        return Vector(P, Q)

Так что же из этого лучше?

Первый подход неудачен как с точки зрения программирования (информация избыточна, реализации методов сложны), так и с точки зрения математики (в которой очень не приветствуются нетрадиционные способы определения равенства, так как равенство обычно является частью логики — того «железа», на котором математика работает).

Второй подход общепринят в математике, но с трудом применим в программировании из-за необходимости общения с бесконечными множествами.

Третий же подход (и некоторые его модификации) используется в программировании.

Четвёртый подход можно встретить как в математике, так и в программировании, хотя он и не очень популярен (особенно в математике, где не очень любят «заранее фиксируем произвольную точку \(P\)»).

В любом из этих подходов направленный отрезок (пара точек) задаёт некоторый вектор, но сам не является вектором. Вектор, соответствующий направленному отрезку \((A,B)\) договоримся обозначать \(\overrightarrow{AB}\).

Небольшое лирическое отступление: разница между вторым и четвёртым подходами ровно та же, что и разница между «назовём рациональным числом максимальное по вложению множество пар целых чисех (второе из которых не равно нулю), в котором любые две пары \(a,b\) и \(x,y\) связаны соотношением \(ay=bx\)» и «назовём рациональным числом пару из целого и целого положительного числа, НОД которых равен 1».

Разложение по базису

Пусть вектора \(e_1, e_2\) соответствуют непараллельным направленным отрезкам. Тогда для любого вектора \(v\) существует единственная пара действительных чисел \(v_1, v_2\), для которой

\[ v = v_1 e_1 + v_2 e_2 \]

Такое представление вектора \(v\) называется разложением по базису \(e_1, e_2\), а сами числа \(v_1\) и \(v_2\) — координатами вектора \(v\) в базисе \(e_1, e_2\).

Не следует путать понятия координат точки и координат вектора. Кроме того, что точки и векторы — объекты разной природы, есть ещё следующие соображения:

• координаты точки требуют наличия системы координат — невырожденного треугольника
• координаты вектора требуют наличия базиса — пары непараллельных векторов

Причём если для любой системы координат \(ABC\) есть традиционный базис, ей соответствующий — вектора \(\overrightarrow{AB}\) и \(\overrightarrow{AC}\) — то ни для какого базиса нет какой-то определённой ассоциированной с ним системы координат.

Движения и некоторые другие преобразования

Напомним, что движением называется отображение плоскости в себя (т.е. функция, принимающая на вход точку плоскости и возвращающая точку плоскости), сохраняющее расстояния между парами точек.

Говоря псевдокодом, это такая функция f, что для любых точек A и B выполнено

distance(f(A), f(B)) == distance(A, B)

Зададимся вопросом о том, как можно задать движение \(f\) плоскости при помощи набора чисел.

Фиксируем некоторый треугольник \(ABC\) и обозначим \(e_1 = \overrightarrow{AB}\) и \(e_2 = \overrightarrow{AC}\).

Введём также обозначения \(X=f(A)\), \(Y=f(B)\), \(Z=f(C)\), \(f_1 = \overrightarrow{XY}\) и \(f_2 = \overrightarrow{XZ}\).

Рассмотрим точку \(P\) с координатами \(p_1, p_2\) в системе координат \(ABC\). Это можно записать в терминах векторов так:

\[ \overrightarrow{AP} = p_1 e_1 + p_2 e_2 \]

Поскольку движение \(f\) не меняет расстояния между точками, расстояния от \(f(P)\) до \(X, Y, Z\) равны соответственно расстояниям от \(P\) до \(A, B, C\). А ещё они же равны расстояниям до \(X, Y, Z\) от точки \(Q\), определённой равенством

\[ \overrightarrow{XQ} = p_1 f_1 + p_2 f_2 \]

Вспомнив о том, что тройка расстояний однозначно задаёт точку, получаем, что \(f(P) = Q\).

Заметив равенство \(\overrightarrow{AQ} = \overrightarrow{AX} + \overrightarrow{XQ}\), получаем, что для того, чтобы узнать координаты вектора \(\overrightarrow{AQ}\) в базисе \(e1, e2\) (они же — координаты точки \(Q\) в системе координат \(ABC\)), достаточно знать координаты векторов \(\overrightarrow{AX}\) и \(\overrightarrow{XQ}\) в этом же базисе.

Разложим \(f_1\), \(f_2\) и \(\overrightarrow{AX}\) по базису \(e1, e2\):

\[ \begin{aligned} f_1 & = f_{11} e_1 + f_{12} e_2 \\ f_2 & = f_{21} e_1 + f_{22} e_2 \\ \overrightarrow{AX} & = x_1 e_1 + x_2 e_2 \end{aligned} \]

Подставив эти разложения в выражение для \(\overrightarrow{AQ}\), получим

\[ \begin{aligned} \overrightarrow{AQ} & = (p_1 f_{11} + p_2 f_{21} + x_1)e_1 \\ & + (p_1 f_{12} + p_2 f_{22} + x_2)e_2 \end{aligned} \]

Набор чисел

\[ M = \begin{pmatrix} f_{11} & f_{21} & x_1 \\ f_{12} & f_{22} & x_2 \end{pmatrix} \]

называется матрицей преобразования \(f\). Такими матрицами при помощи вышеприведённой формулы можно задавать не только движения, но и другие преобразования (растяжения и скосы). Класс преобразований, задающихся формулой

\[ \begin{aligned} \overrightarrow{AQ} & = (p_1 f_{11} + p_2 f_{21} + x_1)e_1 \\ & + (p_1 f_{12} + p_2 f_{22} + x_2)e_2 \end{aligned} \]

называется линейными неоднородными преобразованиями.

Поэкспериментировать с ними можно в демонстрации.

Напоследок скажем, что, к сожалению, нет устоявшегося соглашения о том, как именно следует ставить эти 6 чисел в таблицу. Единственное более-менее общепринятое соглашение — о нумерации строк и столбцов таблицы:

\[ M = \begin{pmatrix} M_{11} & M_{12} & M_{13} \\ M_{21} & M_{22} & M_{23} \end{pmatrix} \]

То есть, в наших обозначениях \(M_{11} = f_{11}\), \(M_{12} = f_{21}\), \(M_{13} = x_{1}\), \(M_{21} = f_{12}\), \(M_{22} = f_{22}\), \(M_{23} = x_{2}\).

Приложение А (о понятии линейности)

Вообще говоря, в математике есть «широкое» понятие линейного преобразования. Так называется преобразование \(f\) векторных простанств, т.е. преобразующее вектор в вектор (возможно, другой природы), удовлетворяющее равенству

\[ f(\alpha u + \beta v) = \alpha f(u) + \beta f(v) \]

для любой пары чисел \(\alpha,\beta\) и пары векторов \(u\) и \(v\).

Нетрудно заметить, что преобразование, преобразующее вектор \(v = v_1 e_1 + v_2 e_2\) по формулам

\[ \begin{aligned} f(v) & = (v_1 f_{11} + v_2 f_{21})e_1 \\ & + (v_1 f_{12} + v_2 f_{22})e_2 \end{aligned} \]

является линейным.

Более того, любое линейное преобразование (векторов плоскости) можно задать такой формулой: поскольку для всех \(v_1\) и \(v_2\) выполнено

\[ f(v_1 e_1 + v_2 e_2) = v_1 f(e_1) + v_2 f(e_2) \]

то, зная \(f(e_1)\) и \f(e_2)\), мы знаем, во что преобразуется любой вектор. Соответственно, числа \(f_{ij}\) из вышеприведённой формулы для \(f(v)\) получаются путём разложения \(f(e_i)\) по базису:

\[ \begin{aligned} f(e_1) & = f_{11} e_1 + f_{12} e_2 \\ f(e_2) & = f_{21} e_1 + f_{22} e_2 \end{aligned} \]

Теперь, наконец, заметим что линейные преобразования векторов (ЛПВ) — это совсем не то же самое, что и рассмотренные нами выше линейные неоднородные преобразования плоскости (ЛНПП):

• ЛПВ преобразуют вектора в вектора, ЛНПП — точки плоскости — в точки плоскости
• даже если отоджествить точки плоскости с их радиус-векторами (относительно некоторого «начала»), ЛПВ не позволяют моделировать сдвиги

Приложение Б (о проективной геометрии)

В том случае, когда уж очень хочется оставаться в рамках линейных преобразований векторов (например, по той причине, что про них есть такая огромная область математики как линейная алгебра), можно воспользоваться следующим трюком:

• увеличить размерность пространства на 1 (т.е. рассмотреть вместо плоскости трёхмерное пространство)
• выбрать в нём плоскость \(\pi\) и точку \(P\), не лежащую в ней
• на множестве всех векторов ввести операцию «проекции»:
  • если вектор \(v\) параллелен \(\pi\), то сопоставим ему вектор плоскости \(\pi\), соответствующий направленному отрезку, лежащему в \(pi\) и задающему \(v\) в пространстве
  • если же вектор \(v\) не параллелен \(\pi\), то сопоставим ему точку пересечения прямой, проведённой из \(P\) и параллельной \(v\), с плоскостью \(\pi\)
• при этом обычно выбирают систему координат \(PABC\), в которой \(PA\), \(PB\) и \(PC\) равны по длине и перпендикулярны друг другу, причём \(C\) находится в плоскости \(\pi\)
• при таком выборе проекция векторов, не параллельных \(\pi\) — просто отображение вида \((x,y,z)\mapsto (x/z, y/z, 1)\)

У этого подхода очень много привлекательных сторон:

• теперь сдвиги — тоже линейные преобразования (трёхмерных) векторов
• можно моделировать как точки, так и вектора плоскости тройками чисел без вероятности их перепутать: у векторов третья координата 0, у точек же она ненулевая
• если для всех точек определить канонические координаты как те, у которых третья компонента равна 1, то получим удобные соотношения вида «разность точек является вектором» и «сумма точки и вектора является точкой»

Но есть и недостатки:

• теперь у одной и той же точки есть бесконечно много троек чисел, ей соответствующих
• три числа больше, чем два (и менее эффективно с вычислительной точки зрения)
• нет единого соглашения о том, отличать ли точки с отрицательной третьей координатой от таковых с положительной:
  • математики предпочитают считать, что отличать не нужно (более того, они отождествляют даже параллельные \(\pi\) вектора, если эти вектора параллельны друг другу, а нулевой вектор вообще выкидывают)
  • программисты же чаще различают такие точки, чем нет (и по факту работают не с «проективной плоскостью» в общематематическом смысле, а просто — с парой или тройкой обычных плоскостей)

В заключение отметим, что та матрица \(3\times 3\), которая изображена на MDN в документации к методу setTransform

\[ \begin{pmatrix} f_{11} & f_{21} & x_1 \\ f_{12} & f_{22} & x_2 \\ 0 & 0 & 1 \end{pmatrix} \]

это — именно матрица линейного преобразования проективной геометрии. И применяется она к вектору \(p_1 e_1 + p_2 e_2 + 1 e_3\), который соответствует точке плоскости с координатами \((p_1, p_2)\).

Облака точек

В процессе написания

Код с урока

Его нужно дописать до чего-нибудь интересного.

Новый код

Он уже дописан до чего-то интересного.

Если у кого-то есть вопросы о том, что там происходит, то пока тезисно:

• рисуем границу «облака точек»
• для этого каждую из точек облака «штампуем» на квадратную сетку
• форма «кисти» называется функцией влияния
• у нас влияние радиально (убывает в зависимости от расстояния до точки)
• после того, как мы учли влияние всех точек облака на сетку, про облако забываем
• те узлы сетки, в которых влияние достаточно большое, считаем находящимися внутри облака
• остальные узлы считаем находящимися снаружи
• для каждой клетки сетки в зависимости от того, какие её узлы находятся внутри облака, а какие — снаружи (всего 16 случаев), строим отрезки границы

Именно последний пункт называется марширующими квадратами, и как раз он (а точнее, его цикл по всем клеткам сетки) отсутствует в коде по ссылке (также там отсутствует значительная часть таблицы, показывающей, какие стороны клетки нужно соединять отрезками в каком из случаев).

Трёхмерная графика

Этот раздел — основная часть курса. Поэтому без лишних слов предлагаем просто перейти к первому его подразделу.

Геометрическая алгебра

Здесь речь пойдёт о геометрической алгебре — науке, изучающей алгебраические свойства некоторых геометрических объектов.

Не следует путать геометрическую алгебру с гораздо более сложной и абстрактной алгебраической геометрией — наукой, изучающей геометрические свойства некоторых алгебраических объектов.

Произведения в алгебре

Основные операции в алгебре — сумма и произведение. Какие бы действия этими словами не назывались, обычно от них требуют выполнения распределительных законов:

\[ \begin{aligned} a(x+y) & = ax + ay \\ (a+b)x & = ax + bx \end{aligned} \]

Почти никаких других свойств обычно не требуют, но некоторые прилагаются к распределительным законам более-менее забесплатно.

Например, если есть «единица» — такой объект \(e\), что

\[ ae = ea = a \]

то, если сложение обладает сочетательным законом, выполняется равенство

\[ x + x + y + y = x(e+e) + y(e+e) = (x+y)(e+e) = (x+y)e + (x+y)e = x + y + x + y \]

откуда при возможности сокращения на \(x+\square\) и \(\square+y\) следует переместительный закон сложения:

\[ x + y = y + x \]

Как мы уже знаем, в геометрии широко используются векторы, которые можно складывать между собой и растягивать в числовой коэффициент раз.

А вот о произведении векторов между собой не говорят. Причём по очень простой причине: разных способов ввести осмысленное произведение существует очень много, причём все они обладают билинейностью — расширенной версией распределительных законов: а именно, для любых чисел \(\alpha\) и \(\beta\) выполнено

\begin{aligned} a(\alpha x + \beta y) & = \alpha ax + \beta ay \\ (\alpha a + \beta b)x & = \alpha ax + \beta bx \end{aligned}

Наиболее полезные из произведений мы и рассмотрим в этом разделе. Договоримся при этом, что у нас заранее фиксирован некоторый ортонормированный базис \(e_1\), \(e_2\), \(e_3\). Ортонормированность означает, что вектора перпендикулярны друг другу и все они единичной длины.

Таблица умножения

Заметим, что из билинейности следует, что произведение любой пары векторов можно однозначно задать, задав произведения базисных:

\[ (a_1e_1 + a_2e_2 + a_3e_3)(b_1e_1 + b_2e_2 + b_3e_3) = \sum_{ij} (a_ia_j)(e_ie_j) \]

Зная \(e_ie_j\), мы можем по этой формуле вычислить произведение любой пары векторов.

Скалярное произведение

Обычно обозначается точкой. Результат — число. Имеет следующую таблицу умножения:

\[ \begin{matrix} e_1\cdot e_1 = 1 & e_1\cdot e_2 = 0 & e_1\cdot e_3 = 0 \\ e_2\cdot e_1 = 0 & e_2\cdot e_2 = 1 & e_2\cdot e_3 = 0 \\ e_3\cdot e_1 = 0 & e_3\cdot e_2 = 0 & e_3\cdot e_3 = 1 \end{matrix} \]

Из этой таблицы следует общая формула

\[ (a_1e_1 + a_2e_2 + a_3e_3)\cdot(b_1e_1 + b_2e_2 + b_3e_3) = a_1b_1 + a_2b_2 + a_3b_3 \]

В частности, если \(a_i = b_i\), получается сумма квадратов координат вектора, что, согласно теореме Пифагора, является длиной этого вектора. Поэтому сформулируем

Свойство №1: скалярный квадрат есть квадрат длины

\[ a\cdot a = |a|^2 \]

Далее заметим, что из явной формулы сразу следует

Свойство №2: скалярное произведение коммутативно

\[ a\cdot b = b\cdot a \]

Пусть теперь вектора \(a\) и \(b\) перпендикулярны друг другу. Тогда

\[ (a+b)\cdot(a+b) = |a+b|^2 = \text{по т. Пифагора} = |a|^2 + |b|^2 = a\cdot a + b\cdot b \]

Если мы теперь раскроем скобки в левой части и сократим обе части на \(a\cdot a\) и \(b\cdot b\), то останется

\[ a\cdot b + b\cdot a = 0 \]

А из того, что \(a\cdot b = b\cdot a\), сразу следует

Свойство №3: скалярное произведение перпендикулярных векторов равно нулю

\[ a\cdot b = 0,\;\text{если \(a\) и \(b\) перпендикулярны} \]

Пусть теперь \(a\) и \(b\) — два произвольных вектора, причём \(b\) ненулевой. Обозначим \(A\) проекцию вектора \(a\) на вектор \(b\). Заметим, что тогда вектор

\[ c = a - \frac{A}{|b|}b \]

перпендикулярен вектору \(b\). Поэтому \(c\cdot b = 0\). Раскрывая в этом равенстве \(c\) по определению, получаем

\[ a\cdot b - \frac{a}{|b|}|b|^2 = 0 \]

откуда следует

Свойство №4: скалярное произведение векторов равно произведению проекции одного из них на другой и длины другого

что, с учётом \(A=|a|\cos\angle(a,b)\) можно записать как

\[ a\cdot b = |a||b|\cos\angle(a,b) \]

откуда следует

Свойство №5: если скалярное произведение ненулевых векторов равно нулю, то они перпендикулярны

Каких свойств нет?

Нет, к сожалению, сочетательного закона: результат — число, которое нельзя скалярно умножить на вектор.

Более того, если даже скалярным произведением числа на вектор считать растяжение, сочетательного закона всё равно нет:

\[ e_2 = (e_1\cdot e_1) e_2 \ne e_1 (e_1\cdot e_2) = 0 e_1 \]

Векторное произведение

Обычно обозначается крестиком. Результат — вектор.

Имеет следующую таблицу умножения:

\[ \begin{matrix} e_1\times e_1 = 0 & e_1\times e_2 = e_3 & e_1\times e_3 = -e_2 \\ e_2\times e_1 = -e_3 & e_2\times e_2 = 0 & e_2\times e_3 = e_1 \\ e_3\times e_1 = e_2 & e_3\times e_2 = -e_1 & e_3\times e_3 = 0 \end{matrix} \]

Из этой таблицы следует общая формула

\[ \begin{aligned} (a_1e_1 + a_2e_2 + a_3e_3)\times(b_1e_1 + b_2e_2 + b_3e_3) & = e_1 (a_2b_3 - a_3b_2) \\ & + e_2 (a_3b_1 - a_1b_3) \\ & + e_3 (a_1b_2 - a_2b_1) \end{aligned} \]

Из этой формулы сразу следует

Свойство №1: векторный квадрат любого вектора нулевой

\[ a\times a = 0 \]

Более того, из \(a\times b = 0\) следует, что \(a\) и \(b\) параллельны.

Также из общей формулы сразу следует

Свойство №2: векторное произведение антикоммутативно

\[ a\times b = -b\times a \]

А ещё путём нехитрых вычислений из общей формулы можно получить

Свойство №3: векторное произведение перпендикулярно любому из сомножителей

\[ \begin{aligned} (a\times b) \cdot a & = 0 \\ (a\times b) \cdot b & = 0 \end{aligned} \]

Любители алгебры также могут, вычислив скалярный квадрат векторного произведения, без особого труда доказать

Свойство №4: длина векторного произведения перпендикулярных векторов равна произведению их длин

\[ |a\times b| = |a||b|,\;\text{если \(a\) и \(b\) перпендикулярны} \]

Применив это соображение к вектору \(c\) построенному по паре произвольных \(a\) и \(b\) по рецепту из разговора про скалярное произведение, получим

\[ |a\times b| = |c\times b| = |c||b| \]

что с учётом очевидного соотношения \(|c|=|a|\sin\angle(a,b)\) даёт

Свойство №5: длина векторного произведения равна произведению длин векторов, помноженному на синус угла между ними

\[ |a\times b| = |a||b|\sin\angle(a, b) \]

Каких свойств нет

Нет, к сожалению, сочетательного закона, хотя теперь с типами всё нормально. Вместо него есть тождество Якоби:

\[ (a\times b)\times c + (b\times c)\times a + (c\times a)\times b = 0 \]

Тензорное произведение

Вводится исходя из позиции: «нам нужен сочетательный закон, поэтому к чёрту все остальные свойства!»

Для любой последовательности \(\alpha\) чисел из набора от 1 до 3 введём «базисный» тензор \(e_{\alpha}\) (сюда, конечно же, входят наши \(e_1\), \(e_2\), \(e_3\)). Рангом такого тензора будем называть длину последовательности индексов. Например, базисные вектора — тензоры ранга 1.

(Градуированным) тензором будем называть взвешенную сумму таких базисных тензоров (две суммы равны тогда и только тогда, когда равны результаты «приведения подобных»).

Таблица умножения содержит бесконечное множество ячеек вида

\[ e_{\alpha}\otimes e_{\beta} = e_{\alpha\beta} \]

Например,

\[ (1e + 2e_2)\otimes(3e_{23}+4e_{2}) = 3e_{23} + 6e_{223} + 4e_{2} + 8 e_{22} \]

Какие свойства есть?

Есть сочетательный закон

\[ (a\otimes b)\otimes c = a\otimes(b\otimes c) \]

Никуда не делась билинейность (при помощи которой мы определяем произведение произвольных взвешенных сумм базисных тензоров).

Каких свойств нет?

Да никаких интересных, кроме сочетательного закона и билинейности. Также нет никакого геометрического смысла (а что могла бы означать сумма \(3e + 2e_{1} - 7 e_{1332121}\)?)

Полезное соглашение

Как в многочленах никто без надобности не пишет \(ax^0\), так и в тензорах вместо \(ae\), где \(a\) — число, все обычно пишут просто \(a\).

Геометрическое произведение

Обозначается либо никак, либо знаком ⟑. Мы будем обозначать геометрическое произведение никак.

Для того, чтобы ввести геометрическое произведение, нам понадобится понятие строго упорядоченного базисного тензора (СУБТ). Назовём СУБТ базисный тензор, у которого последовательность индексов строго упорядочена.

В трёхмерном пространстве есть всего 8 СУБТ:

• один — ранга 0: \(e\)
• три — ранга 1: \(e_1\), \(e_2\), \(e_3\)
• три — ранга 2: \(e_{12}\), \(e_{13}\), \(e_{23}\)
• один — ранга 3: \(e_{123}\)

Входы: взвешенные суммы СУБТ. Результат: тензор, который тоже является взвешенной суммой СУБТ.

Можно было бы выписать всю таблицу умножения, но мы вместо этого сформулируем процедуру вычисления произведения \(e_{\alpha}e_{\beta}\):

• сортируем последовательность \(\alpha\beta\) путём обменов
• считаем чётность количество обменов
• выкидываем из неё все пары одинаковых чисел; то, что осталось, назовём \(\gamma\)
• если обменов было чётное число, то результат \(e_{\gamma}\)
• если же обменов было нечётное число, то результат \(-e_{\gamma}\)

Например, \(e_{12}e_{13}\) можно вычислить так:

• отсортированная последовательность \(1123\)
• пузырёк делает ровно один обмен; это — нечётное число
• \(\gamma = 23\)
• результат: \(-e_{23}\)

Конечно, открытым остаётся вопрос о том, почему чётность количества обменов не зависит от способа сортировки. Тем не менее, ответ на этот вопрос прост: каждый обмен изменяет чётность количества пар элементов, стоящих в неправильном порядке — таких пар, в которых правый элемент меньше левого.

Свойство №1: сочетательный закон

Как ни странно, но вышеописанная процедура умножения СУБТ ассоциативна. Поэтому и для произвольных сумм СУБТ выполнено

\[ (ab)c = a(bc) \]

Вариации

То, что мы описали выше, называется \((3,0,0)\)-произведением. В общем случае \((a,b,c)\)-произведение определяется в \((a+b+c)\)-мерном пространстве такой же процедурой за исключением шага с удалением дубликатов:

• за каждый дубликат чисел от \(a+1\) до \(a+b\) нужно результат домножить на \(-1\)
• если есть хотя бы один дубликат числа от \(a+b+1\) до \(a+b+c\), то результат равен 0

Независимо от типа, любое такое произведение обладает сочетательным законом.

Произведения типа \((3,1,0)\) используются в теории относительности, а типа \((3,0,1)\) — в проективной геометрической алгебре. Нам же сейчас понадобится \((0,0,3)\)-произведение.

Внешнее произведение

Это самое \((0,0,3)\)-произведение называется внешним и обозначается \(\wedge\).

Нетрудно получить явную формулу для внешнего произведения векторов:

\[ \begin{aligned} (a_1e_1 + a_2e_2 + a_3e_3)\wedge(b_1e_1 + b_2e_2 + b_3e_3) & = e_{12} (a_1b_2 - a_2b_1) \\ & + e_{13} (a_1b_3 - a_3b_1) \\ & + e_{23} (a_2b_3 - a_3b_2) \end{aligned} \]

Не правда ли, похожа на таковую для векторного произведения? Причём внешнее произведение, в отличие от векторного, имеет сочетательный закон!

Из этой формулы сразу следуют

Свойство №2: внешнее произведение вектора с самим собой равно 0

\[ a\wedge a = 0 \]

Более того, из \(a\wedge b = 0\) следует, что вектора \(a\) и \(b\) параллельны.

Это позволяет сразу договориться о геометрическом смысле внешнего произведения.

Поскольку

\[ a\wedge b = (a + tb)\wedge b \]

для любого числа \(t\), а подобными преобразованиями из пары непараллельных векторов можно сделать пару непараллельных векторов любых направлений (где под «направлением» понимается прямая, а не луч), можно заключить следующее: если пара векторов \(a, b\) задаёт ту же плоскость, что и пара векторов \(u, v\), то произведения \(a\wedge b\) и \(u\wedge v\) пропорциональны друг другу.

Более того, если пары векторов \(a, b\) и \(u, v\) задают разные плоскости, то произведения \(a\wedge b\) и \(u\wedge v\) не пропорциональны. Действительно, из этих пар векторов преобразованиями вышеуказанного вида сделать пары, в которых первые вектора параллельны друг другу. Пусть эти пары \(p, q\) и \(\alpha p, r\). Нетрудно заметить, что если бы произведения были бы пропорциональны:

\[ p \wedge q = \beta (\alpha p \wedge r) \]

то их разность, имеющая вид

\[ p \wedge (q - \alpha\beta r) \]

была бы нулевой. А это означало бы, что \(q - \alpha\beta r\) пропорционально \(p\). То есть \(q\) лежало бы в той же плоскости, что и \(p\) с \(r\). Что противоречит предположению о том, что пары \(a,b\) и \(u,v\) задают разные плоскости.

Итого имеем

Геометрический смысл внешнего произведения векторов: это (с точностью до пропорциональности) — плоскость, в которой лежат сомножители

Более того, любая взвешенная сумма СУБТ второго ранга является внешним произведением пары векторов. Действительно, если рассмотреть ненулевую сумму

\[ x_{12} e_{12} + x_{13} e_{13} + x_{23} e_{23} \]

то ей пропорционально внешнее произведение любой пары из следующих векторов:

• \(x_{13} e_1 + x_{23} e_2\)
• \(x_{23} e_3 - x_{12} e_1\)
• \(x_{13} e_3 + x_{12} e_2\)

два из которых заведомо ненулевые.

Свойство №3: внешнее произведение пары векторов антикоммутативно

\[ a\wedge b = -b\wedge a \]

Тут следует быть внимательным: для невекторов это неверно. Как нетрудно заметить, \(e_{12}\wedge e_{3} = e_{123} = e_{3}\wedge e_{12}\), поскольку последовательность \(312\) сортируется двумя обменами.

Наконец, главное свойство геометрической алгебры (следует из явных формул для геометрического и внешнего произведений)

Свойство №4: геометрическое произведение пары векторов есть сумма их скалярного и внешнего произведений

\[ ab = a\cdot b + a\wedge b \]

В частности, если \(a\) и \(b\) перпендикулярны, то их геометрическое произведение совпадает со внешним.

Свойство №5: геометрическое произведение вектора с самим собой есть квадрат его длины

\[ a^2 = |a|^2 \]

Вращения плоскости и пространства

Пусть \(a\) и \(b\) — ортонормированные вектора. Заметим следующую пару соотношений:

\[ \begin{aligned} a(ab) & = aab = b \\ b(ab) & = bab = -abb = -a \end{aligned} \]

То есть умножение на \(ab\) справа поворачивает вектора \(a\) и \(b\) (и, как следствие, — любой вектор плоскости, в которой лежат \(a\) и \(b\)) на прямой угол по направлению от \(a\) к \(b\).

Поскольку поворот на угол \(\alpha\) можно скомбинировать из тождественного преобразования и поворота на прямой угол, получаем

Формулу №1: поворот векторов плоскости

Отображение

\[ v \mapsto v(\cos\alpha + ab\sin\alpha) \]

поворачивает вектор \(v\), лежащий в плоскости ортонормированной пары \(a, b\), на угол \(\alpha\) по направлению от \(a\) к \(b\).

Если нам нужно соединить два поворота, то достаточно перемножить

\[ (\cos\alpha + ab\sin\alpha)(\cos\beta + ab\sin\beta) \]

Что интересно, такое произведение — наиболее простой способ запомнить (или доказать) формулы косинуса и синуса суммы углов.

Лирическое отступление: алгебра, порождённая действительными числами и СУБТ \(e_{12}\) (или же любым другим произведением ортонормированной пары векторов) называется комплексными числами и известна примерно со середины 16 века благодаря работам Джероламо Кардано (благодаря ему же нам известны многочисленные применения карданного вала и карданного подвеса, а также — метод решения кубических уравнений). Несколько позже комплексные числа начали использовать для удобного описания вращений плоскости.

Заметив, что умножение справа на \(ab\) воздействует на вектора плоскости так же, как и умножение слева на \(ba\), мы можем получить

Формулу №2: поворот векторов плоскости

Отображение

\[ v \mapsto (\cos\alpha - ab\sin\alpha)v \]

поворачивает вектор \(v\), лежащий в плоскости ортонормированной пары \(a, b\), на угол \(\alpha\) по направлению от \(a\) к \(b\).

Более того, скомбинировав эти два преобразования, можно получить преобразование, которое не изменяет вектора, перпендикулярные плоскости.

А именно, если \(c\) перпендикулярен как \(a\), так и \(b\), то

\[ \begin{aligned} & (\cos\alpha - ab\sin\alpha)c(\cos\alpha + ab\sin\alpha) \\ =\; & c((\cos\alpha)^2 + (\sin\alpha)^2) + abc(\cos\alpha\sin\alpha-\sin\alpha\cos\alpha) \\ =\; & 1c + 0abc \\ =\; & c \end{aligned} \]

Как следствие, имеем

Формулу №3: поворот векторов пространства

Отображение

\[ v \mapsto (\cos(\alpha/2) - ab\sin(\alpha/2))v(\cos(\alpha/2) + ab\sin(\alpha/2)) \]

поворачивает произвольный вектор \(v\) на угол \(\alpha\) по направлению от \(a\) к \(b\).

Конечно, хочется иметь возможность задавать поворот не плоскостью и уголом, а осью и углом. Но это, оказывается, несложно.

А именно, если мы произведём замену

\[ \begin{aligned} e_1 & \mapsto e_2e_3 \\ e_2 & \mapsto e_3e_1 \\ e_3 & \mapsto e_1e_2 \end{aligned} \]

то получим из вектора перпендикулярную ему плоскость (точнее, тензор, являющийся произведением пары векторов, в этой плоскости лежащих).

Чтобы это понять, можно провести следующее рассуждение: рассмотрим тройку ортонормированных векторов \(a,b,c\). Вычислим произведение

\[ (Aa + Bb + Cc)ab \]

где \(A,B,C\) — произвольные числа.

Получим следующее:

\[ Ab - Ba + Cabc \]

Как нетрудно видеть, тензоры первого ранга в таком произведении присутствуют тогда и только тогда, когда вектор не перпендикулярен плоскости.

Осталось вычислить

\[ (x_1 e_1 + x_2 e_2 + x_3 e_3)(x_1 e_2e_3 + x_2 e_3e_1 + x_3e_1e_2) \]

и заметить, что все тензоры первого ранга в итоговой сумме взаимоуничтожатся.

Конечно, остаётся вопрос: при каком условии сумма вида \(x_1 e_2e_3 + x_{2} e_3e_1 + x_{3} e_1e_2\) может быть представлена в виде произведения пары ортонормированных векторов?

Мы дадим ответ: тогда и только тогда, когда \(x^2_1 + x^2_2 + x^2_3 = 1\). А доказательство оставим в качестве тривиального упражнения, напомнив лишь, что:

• любая сумма СУБТ второго ранга представляется в виде внешнего произведения векторов
• внешнее произведение перпендикулярных векторов совпадает с их геометрическим произведением
• если \(a\) и \(b\) перпендикулярны, то \((ab)(ab) = -aabb = -|a|^2 |b|^2\)

Опять лирическое отступление: алгебра, порождённая действительными числами и тензорами \(e_{12}\), \(e_{13}\) и \(e_{23}\), называется алгеброй кватернионов. До развития методов геометрической алгебры именно кватернионы применялись для удобного описания вращений пространства. С кватернионами мы ещё встретимся далее.

Некоторые практические задачи

Решение линейных уравнений

Начнём с одной из важнейших задач — решения линейных уравнений.

Допустим, нам известно, что \(ax = b\), и нужно найти \(x\).

В некоторых случаях подобная задача хорошо решается:

• если \(a\) — ненулевой вектор, то \(|a|^2x = ab\), откуда \(x = ab / |a|^2\)
• если \(a = \alpha + v\), где \(\alpha\) — число, а \(v\) — вектор, то \((\alpha-v)(\alpha + v) = \alpha^2 - |v|^2\); если эта разность отлична от нуля, то \(x = (\alpha-v)b / (\alpha^2 - |v|^2)\)
• аналогично, если \(a = \alpha + t\), где \(t\) — тензор второго ранга, то \(x = (\alpha - t)b / (\alpha^2 + |t|^2)\), где \(|t|^2\) — обозначение для суммы квадратов компонент тензора \(t\) в базисе \(e_{12}\), \(e_{13}\), \(e_{23}\)

Вычисление угла между векторами

Допустим, что \(a\) и \(b\) — вектора, и нам известно их геометрическое произведение \(ab\).

Поскольку \(ab = a\cdot b + a\land b\), то \(ba = a\cdot b - a\land b\) и, зная \(ab\) мы можем вычислить \(ba\) просто поменяв знак во всех компонентах второго ранга.

Это означает, что мы можем вычислить \(|a|^2|b|^2 = (ba)(ab)\).

А, зная произведение длин векторов, мы легко можем узнать косинус угла между ними: он равен \(a\cdot b / |a||b|\).

Простейшая программа

В этом разделе мы воспользуемся OpenGL и геометрической алгеброй для реализации вращающегося куба.

WebGL-контекст

До этого мы использовали контекст 2d, который давал доступ к некоторым относительно высокоуровневым примитивам. Сейчас мы будем использовать контекст webgl2, который даёт доступ к функциям OpenGL.

let GL = null;

onload = () => {
    ...
    const canvas = document.getElementById(`идентификатор`);
    canvas.width = 600;
    canvas.height = 600;

    GL = canvas.getContext(`webgl2`);
    ...
}

В данном случае мы для простоты привязали контекст к глобальной переменной.

Но следует помнить о том, что использование локальной переменной для контекста помогает отделить те функции, которые занимаются непосредственно взаимодействием с видеокартой, от тех, которые этим не занимаются.

Минимальная анимация

Чтобы убедиться, что всё работает, в конец инициализации добавим

const renderFrame = time => {
    GL.clearColor((1 + Math.cos(time/1000))/2, 0, 0, 1);
    GL.clear(GL.COLOR_BUFFER_BIT | GL.DEPTH_BUFFER_BIT);

    requestAnimationFrame(renderFrame);
};

requestAnimationFrame(renderFrame);

Функция браузера requestAnimationFrame получает на вход функцию и откладывает её выполнение до того момента, как браузер не будет готов нарисовать очередной кадр (обычно браузер рисует кадры с частотой около 60 кадров в секунду).

В тот момент, когда браузер будет готов, отложенная функция будет вызвана, а её на вход подано время, прошедшее с момента запуска программы (выраженное в милисекундах).

Куб

Сначала сформируем данные для рисования куба в оперативной памяти компьютера. Договоримся, что каждая вершина будет задаваться тройкой координат и её номером (от которого будет зависеть её цвет).

function makeCube() {
    const v0 = [-1, -1, -1, 0];
    const v1 = [-1, -1,  1, 1];
    const v2 = [-1,  1, -1, 2];
    const v3 = [-1,  1,  1, 3];
    const v4 = [1,  -1, -1, 4];
    const v5 = [1,  -1,  1, 5];
    const v6 = [1,   1, -1, 6];
    const v7 = [1,   1,  1, 7];

    return Float32Array.from(
        v0.concat(v1).concat(v2)
        .concat(v1).concat(v2).concat(v3)
        .concat(v0).concat(v1).concat(v4)
        .concat(v1).concat(v4).concat(v5)
        .concat(v0).concat(v2).concat(v4)
        .concat(v2).concat(v4).concat(v6)
        .concat(v7).concat(v3).concat(v6)
        .concat(v3).concat(v6).concat(v2)
        .concat(v7).concat(v5).concat(v3)
        .concat(v5).concat(v3).concat(v1)
        .concat(v7).concat(v5).concat(v6)
        .concat(v5).concat(v6).concat(v4)
    ); 
}

Эта функция выдаёт типизированный массив (все его числа хранятся в памяти в стандартном формате одинарной точности). Именно такой массив затем можно записать в память видеокарты.

Для того, чтобы переписать эти данные в память видеокарты, можно воспользоваться следующим кодом:

const buffer = GL.createBuffer();

GL.bindBuffer(GL.ARRAY_BUFFER, buffer);
GL.bufferData(GL.ARRAY_BUFFER, makeCube(), GL.STATIC_DRAW);

Метод createBuffer создаёт (изначально пустой) массив в памяти видеокарты и возвращает его уникальный идентификатор, а bufferData выделяет память и копирует данные из оперативной памяти компьютера в видеопамять.

Метод bindBuffer — некоторый анахронизм: по какой-то причине bufferData, вместо того, чтобы принимать на вход уникальный идентификатор буфера, принимает на вход специальную константу — текущее назначение буфера. Соответствующий буфер должен при этом быть заранее привязан к этому назначению.

Далее мы ещё встретим несколько функций, которые работают именно с тем буфером, который последним был связан с назначением ARRAY_BUFFER.

Замечание На самом деле, createBuffer всего лишь ищет и возвращает неиспользованный идентификатор, а буфер создаётся во время вызова bindBuffer. Но WebGL этот факт от пользователя тщательно скрывает (и правильно делает). Тем не менее, если об этом помнить, то не будет соблазна один и тот же буфер привязывать при помощи bindBuffer к разным назначениям.

Вершинная и фрагментная программы

Несколько упрощённо процедуру работы видеокарты можно описать следующим образом. Для того, чтобы нарисовать треугольник, она:

• для каждой вершины треугольника забирает из видеопамяти какой-то набор чисел, называемых атрибутами
• к этим атрибутам применяет программу, называемую термином вершинный шейдер
• вершинный шейдер выдаёт положение вершины в пространстве и некоторый набор выходных атрибутов
• по положениям вершин вычисляется положение треугольника на экране, к каждому пикселю этого треугольника применяет фрагментный шейдер
• фрагментному шейдеру доступны выходные атрибуты вершинного, линейно инетрполированные из соответствующей тройки вершин (под линейной интерполяцией понимается взвешенная сумма значений, веса в которой — доли, которые составляют площади треугольников, две стороны каждого из которых проведены от рассматриваемого пикселя к вершинам, противоположным той, про вес чьего значения сейчас идёт речь, по отношению к площади треугольника, образованного всей тройкой вершин)
• фрагментный шейдер выдаёт цвет пикселя (и его глубину — если она оказывается больше, чем последняя выданная этому пикселю глубина, пиксель не рисуется)

Сперва зададим разбиение буфера с вершинами треугольников граней куба на атрибуты:

const coord = 0;
const index = 1;

GL.enableVertexAttribArray(coord);
GL.vertexAttribPointer(coord, 3, GL.FLOAT, false, 16, 0);

GL.enableVertexAttribArray(index);
GL.vertexAttribPointer(index, 1, GL.FLOAT, false, 16, 12);

Метод vertexAttribPointer задаёт связь между указанным атрибутом и буфером, связанным в текущий момент с назначением ARRAY_BUFFER.

Его параметры:

• номер атрибута (нумеруются от нуля и до GL.MAX_VERTEX_ATTRIBS - 1)
• размерность атрибута (от 1 до 4)
• формат данных в памяти
• интерпретация целочисленных форматов (для формата FLOAT не играет роли)
• расстояние между атрибутами соседних вершин в байтах (можно поставить 0; при этом расстояние будет автоматически вычислено как произведение размерности на размер одной единицы данных указанного формата)
• номер начального байта атрибута начальной вершины

Формат FLOAT, как нетрудно заметить, требует 4 байта на число.

Теперь напишем вершинный и фрагментный шейдеры:

Вершинный шейдер

#version 300 es

in vec3 coord;
in float index;

out vec3 color;

void main() {
    vec3 position = coord + vec3(0, 0, 7);
    
    gl_Position = vec4(position.xy, -1, position.z);

    switch (int(index)) {
    case 0:
        color = vec3(0.3, 0.3, 0.3);
        break;
    case 1:
        color = vec3(0.3, 0.3, 0.7);
        break;
    case 2:
        color = vec3(0.3, 0.7, 0.3);
        break;
    case 3:
        color = vec3(0.3, 0.7, 0.7);
        break;
    case 4:
        color = vec3(0.7, 0.3, 0.3);
        break;
    case 5:
        color = vec3(0.7, 0.3, 0.7);
        break;
    case 6:
        color = vec3(0.7, 0.7, 0.3);
        break;
    case 7:
        color = vec3(0.7, 0.7, 0.7);
        break;
    default:
        color = vec3(0, 0, 0);
    }
}

Фрагментный шейдер

#version 300 es
precision highp float;

in vec3 color;
out vec4 frag_color;

void main() {
    frag_color = vec4(color, 1);
}

Особенности шейдеров

Вершинный и фрагментный шейдеры пишутся на языке GLSL, весьма сильно напоминающем язык Си (но не являющимся таковым).

Ключевое отличие GLSL от Javascript и Python — статическая типизация. А именно, каждая переменная, каждая функция и каждая формула имеет тип (в динамически типизированных языках тип имеют только значения формул). В языке Си (и GLSL) объявления переменных выглядят как тип имя_переменной;

Функция main — точка входа в программу (именно она автоматически выполняется при запуске программы). Код вне функций (кроме объявления переменных) запрещён. В качестве типа возвращаемого значения у неё стоит «пустой» тип void.

Перед функцией main определено два входа-атрибута

• in vec3 coord
• in float index

и один выход

• out vec3 color

который путём линейной интерполяции между тройкой вершин будет передан фрагментному шейдеру. Названия этих переменных абсолютно иррелевантны, но входные переменные фрагментного шейдера должны называться так же, как соответствующие им выходы вершинного шейдера.

Основная задача вершинного шейдера — выставить значение глобальной переменной gl_Position. Это — четырёхмерный вектор, компоненты которого имеют следующий смысл:

• смещение вершины вправо от наблюдателя
• смещение вершины вверх от наблюдателя
• необработанная глубина вершины
• смещение вершины вдаль от наблюдателя

Полученный треугольник проецируется на экран, который отождествляется с квадратом \(2\times 2\), удалённым от наблюдателя вдаль на 1. Центр этого квадрата имеет в качестве экранных координат пару нулей. Экранные координаты правого верхнего края — пара единиц.

Задача фрагментного шейдера — выставить цвет — значение глобальной переменной типа out vec4, название которой произвольно (и задаётся в соответствующей строчке программы).

В отличие от вершинного шейдера, во фрагментном требуется явно задать точность вычислений командой precision. Например, команда

precision highp float;

задаёт для чисел типа float точность не ниже стандартной одинарной (1 бит знака, не менее 8 бит экспоненты, не менее 23 бит мантиссы).

Расчёт глубины пикселя

Применяется только если в управляющей программе была включена проверка глубины при помощи команды

GL.enable(GL.DEPTH_TEST);

Фрагментный шейдер может (но не обязан) выставить глубину пикселя — значение глобальной переменной gl_FragDepth. Оно должно быть в пределах от 0 до 1 (значения вне этих границ заменяются на соответствующую границу).

Если фрагментный шейдер не выставляет gl_FragDepth, то используется величина, вычисленная при помощи необработанных глубин соответствующей тройки вершин:

• каждая необработанная глубина делится на её смещение вдаль
• полученные глубины линейно интерполируются по спроецированному на экран треугольнику

Для того, чтобы таким образом вычисленные глубины пикселей получались линейно зависящими от реальных удалений соответствующих им точек от наблюдателя, необработанные глубины тоже должны линейно зависить от удаления вершин от наблюдателя. Говоря проще, если четвёртая координата вершины обозначена \(w\), то формула для вычисления необработанной глубины должна иметь вид

\[ \alpha w + \beta \]

При этом вычисленная глубина будет иметь вид

\[ \alpha + \frac{\beta}{W} \]

где \(W\) — смещение точки, соответствующей пикселю, вдаль от наблюдателя.

Вычисленная глубина допускается в пределах от -1 до 1 (и линейно отображается на диапазон от 0 до 1: если d — вычисленная глубина, то по умолчанию gl_FragDepth = (1.0+d)/2.0;).

Если не хочется задумываться над видом формулы, можно взять просто \(\alpha=0\) и \(\beta = -1\) или \(\alpha=\beta=1\).

При этом точки, расположенные между наблюдателем и экраном (напомним, что экран находится на удалении 1 от наблюдателя) рисоваться не будут.

Внимание! Независимо от того, включена ли проверка глубины, и выставлен ли явно gl_FragDepth, по умолчанию не рисуются все точки, у которых вычисленная глубина оказывается вне диапазона от -1 до 1.

Сборка программы

Для того, чтобы использовать вершинный и фрагментный шейдеры, их нужно «собрать» в единую «программу». Далее мы будем называть шейдеры и результат их сборки управляемыми программами, а программу, которая их собирает и запускает (и которую мы сейчас пишем на Javascript) — управляющей.

Собрать шейдеры можно сделать при помощи следующих функций:

function compileShader(source, type) {
    let glType = type;

    if (type === 'vertex') { glType = GL.VERTEX_SHADER; }
    else if (type === 'fragment') { glType = GL.FRAGMENT_SHADER; }

    const shader = GL.createShader(glType);

    GL.shaderSource(shader, source);
    GL.compileShader(shader);


    if (!GL.getShaderParameter(shader, GL.COMPILE_STATUS)) { 
        console.error(`SHADER TYPE ${type}`);
        console.error(GL.getShaderInfoLog(shader));

        return null;
    }

    return shader;
}


function buildProgram(vsSource, fsSource, attributes) {
    const vs = compileShader(vsSource, 'vertex');
    if (vs === null) { return null; }

    const fs = compileShader(fsSource, 'fragment');
    if (fs === null) { return null; }

    const program = GL.createProgram();

    for (const name in attributes) {
        const index = attributes[name];

        GL.bindAttribLocation(program, index, name);
    }
    
    GL.attachShader(program, vs);
    GL.attachShader(program, fs);
    GL.linkProgram(program);

    if (!GL.getProgramParameter(program, GL.LINK_STATUS)) { 
        console.error(GL.getProgramInfoLog(program));

        return null;
    }

    return program;
}

Единственное интересное место этих функций — строчка с GL.bindAttribLocation. Эта функция устанавливает соответствие между названиями входов вершинного шейдера (глобальных переменных с типом, начинающимся с in) и номерами атрибутов, которые используются в управляющей программе.

Исходники шейдеров можно передать в функцию сборки программы, вставив их прямо в Javascript-программу:

const VS_SRC = `#version 300 es
...
`;

const FS_SRC = `#version 300 es
...
`;

Обратите внимание на обратные кавычки текстовых литералов и расположение первой строчки программы.

Итого полный код настройки геометрии сцены имеет вид

const buffer = GL.createBuffer();

GL.bindBuffer(GL.ARRAY_BUFFER, buffer);
GL.bufferData(GL.ARRAY_BUFFER, makeCube(), GL.STATIC_DRAW);

const coord = 0;
const index = 1;

GL.enableVertexAttribArray(coord);
GL.vertexAttribPointer(coord, 3, GL.FLOAT, false, 16, 0);

GL.enableVertexAttribArray(index);
GL.vertexAttribPointer(index, 1, GL.FLOAT, false, 16, 12);

// В этот момент можно сделать GL.bindBuffer(GL.ARRAY_BUFFER, null);
// нужный буфер уже связан с теми атрибутами, которые использует программа.

const program = buildProgram(VS_SRC, FS_SRC, {
    coord, index
});

GL.useProgram(program);

GL.enable(GL.DEPTH_TEST);

Обратите внимание на последнюю строчку: если её забыть, то проверка глубины пикселей будет отключена (попробуйте её закомментировать и посмотреть, что получится).

Осталось сделать единственную вещь — отдать команду на рисование. Для этого нужно после очищения экрана (при помощи GL.clear) выполнить команду

GL.drawArrays(GL.TRIANGLES, 0, 36);

которая приводит к запуску текущей вершинно-фрагментной программы (выбранной при помощи useProgram). Входы drawArrays следующие:

• способ разбиения вершин на треугольники (TRIANGLES — самый простой: каждые три вершины — очередной треугольник)
• номер начальной вершины
• количество вершин

Будьте внимательны! Все включённые на данный момент атрибуты (даже если они не используются программой) должны иметь привязанные к ним при помощи vertexAttribPointer буферы, в которых должно присутствовать достаточное количество данных. В противном случае вызов drawArrays завершится ошибкой.

Упрощение жизни

Часто при рисовании кадра используется много разных программ и много разных массивов данных.

Для того, чтобы по ходу рисования не заниматься нетривиальным переключением атрибутов и перепривязкой буферов, в OpenGL доступна абстракция, называемая VAO (Vertex Array Object).

VAO хранит в себе набор включённых атрибутов и их привязки к буферам.

Если написать функцию

function createCubeVAO(attributes) {
    const vao = GL.createVertexArray(); // слова Object в названии нет!

    GL.bindVertexArray(vao);

    const buffer = GL.createBuffer();

    GL.bindBuffer(GL.ARRAY_BUFFER, buffer);
    GL.bufferData(GL.ARRAY_BUFFER, makeCube(), GL.STATIC_DRAW);
   
    const { coord, index } = attributes;

    GL.enableVertexAttribArray(coord);
    GL.vertexAttribPointer(coord, 3, GL.FLOAT, false, 16, 0);

    GL.enableVertexAttribArray(index);
    GL.vertexAttribPointer(index, 1, GL.FLOAT, false, 16, 12);

    GL.bindVertexArray(null);

    return vao;
}

то далее весь код настройки геометрии сведётся к

function setupScene() {
    const attributes = {
        coord: 0,
        index: 1,
    };

    const program = buildProgram(VS_SRC, FS_SRC, attributes);

    const cube = createCubeVAO(attributes);  

    GL.enable(GL.DEPTH_TEST);

    return { program, cube };
}

а точка входа в программу примет вид

onload = () => {
    const canvas = document.getElementById("CANVAS");
    canvas.width = 600;
    canvas.height = 600;

    GL = canvas.getContext('webgl2');

    const { cube, program } = setupScene();
    
    const renderFrame = time => {
        GL.clearColor((1 + Math.cos(time/1000))/2, 0, 0, 1);
        GL.clear(GL.COLOR_BUFFER_BIT | GL.DEPTH_BUFFER_BIT);

        GL.useProgram(program);
        GL.bindVertexArray(cube);
        GL.drawArrays(GL.TRIANGLES, 0, 36);
        GL.bindVertexArray(null);

        requestAnimationFrame(renderFrame);
    };

    renderFrame(0);
}

Важно! Не забывайте снимать выбор текущего VAO при помощи bindVertexArray(null). Иначе рано или поздно Вы случайно соедините программу, использующую VAO, с программой, не использующей VAO, и часть, не использующая VAO, испортит тот VAO, с которого Вы забыли снять выбор.

Вращение куба

Для того, чтобы вращать куб, будем передавать в шейдеры положение куба и его ориентацию. Чтобы не добавлять к каждой вершине одни и те же на все вершины данные, можно воспользоваться uniform-входами — их значение задаётся перед вызовом drawArrays и постоянно на всём протяжении процедуры рисования.

Изменим вершинный шейдер (фрагментный трогать не будем — он и так хороший):

#version 300 es

in vec3 coord;
in float index;

out vec3 color;

uniform vec3 axis;
uniform float angle;
uniform vec3 translation;

// t = t.x e12 + t.y e13 + t.z e23 + t.w e
// result = result.x e1 + result.y e2 + result.z e3 + result.w e123
vec4 lapply(vec4 t, vec3 v) {
    return vec4(t.w * v + vec3(
        + t.x * v.y + t.y * v.z,
        - t.x * v.x + t.z * v.z,
        - t.y * v.x - t.z * v.y
    ), t.x*v.z - t.y*v.y + t.z*v.x);
}

// v = v.x e1 + v.y e2 + v.z e3 + v.w e123
vec3 rapply(vec4 v, vec4 t) {
    return t.w * v.xyz + vec3(
        - t.x * v.y - t.y * v.z - t.z * v.w,
        + t.x * v.x - t.z * v.z + t.y * v.w,
        + t.y * v.x + t.z * v.y - t.x * v.w
    );
}

vec3 rotate(vec3 coord, vec3 axis, float angle) {
    axis = normalize(axis);
    float cosine_half = cos(angle / 2.0);
    float sine_half = sin(angle / 2.0);

    vec4 rot_r = vec4(
        sine_half * vec3(axis.z, -axis.y, axis.x),
        cosine_half
    );

    vec4 rot_l = vec4(-rot_r.xyz, rot_r.w);

    return rapply(lapply(rot_l, coord), rot_r);
}

void main() {
    vec3 position = rotate(coord, axis, angle) + translation;
    
    gl_Position = vec4(position.xy, -1, position.z);

    switch (int(index)) { /* всё как и прежде */ }
}

Теперь в нём появились три новые глобальные переменные и функция вращения вокруг заданной оси на заданный угол.

Также модифицируем setupScene:

function setupScene() {
    const attributes = {
        coord: 0,
        index: 1,
    };

    const program = buildProgram(VS_SRC, FS_SRC, attributes);

    const cube = createCubeVAO(attributes);  

    GL.enable(GL.DEPTH_TEST);

    const uniforms = {};

    for (const name of ['axis', 'angle', 'translation']) {
        uniforms[name] = GL.getUniformLocation(program, name);
    }

    return { program, cube, uniforms };
}

Здесь мы получаем идентификаторы соответствующих uniform-переменных из собранной программы (для uniform-ов нет аналога bindAttribLocation; да, впрочем, и не особо нужно — с uniform-ами не связано сложных процедур активации/деактивации и настройки атрибутов).

И, наконец, настройка сцены и рисование кадра примут вид

const { cube, program, uniforms } = setupScene();

const renderFrame = time => {
    GL.clearColor((1 + Math.cos(time/1000))/2, 0, 0, 1);
    GL.clear(GL.COLOR_BUFFER_BIT | GL.DEPTH_BUFFER_BIT);

    GL.useProgram(program);
    
    GL.bindVertexArray(cube);
    
    GL.uniform3f(uniforms.axis, 
        Math.cos(time/3000), 2*Math.cos(time/1700), 3
    );
    GL.uniform1f(uniforms.angle, time/1000);
    GL.uniform3f(uniforms.translation, 0, 0, 7);
    
    GL.drawArrays(GL.TRIANGLES, 0, 36);
    
    GL.bindVertexArray(null);

    requestAnimationFrame(renderFrame);
};

renderFrame(0);

В нём перед каждым актом рисования куба мы выставляем новые значения uniform-входов.

Неквадратный холст

Соглашение о том, что пространство проецируется на квадрат \(-1\leqslant x,y\leqslant 1\), \(w=1\) противоречит возможной неквадратности окна/холста, на котором отображается проекция. Причём неквадратный холст — совершенно типичная ситуация: например, почти у всех дисплеев высота и ширина различаются.

Стандартным выходом в такой ситуации является следующая последовательность действий:

• исходя из каких-то соображений выбирают горизонтальный угол обзора (далее fov); например, у человеческих глаз угол обзора близок к развёрнутому; также популярными являются значения в 90 градусов и 60 градусов
• после формирования горизонтальных координат вершины x и y по ним формируются модифицированные координаты mx и my, по которым и строится gl_Position
• горизонтальная координата получается так: mx = x * tan(fov/2); заметим, что fov должен быть меньше развёрнутого угла; при этом значения fov больше 120 градусов без дополнительной обработки, моделирующей тот факт, что глаз не является плоским, могут выглядеть странно
• вертикальная координата получается так: my = y * tan(fov/2) * aspect, где aspect — отношение горизонтального размера экрана к вертикальному; например, для разрешения \(800\times 600\) требуется aspect=4/3
• если фрагментному шейдеру требуются координаты пикселя (например, для освещения), их нужно передавать как x, y, w (а не как mx, my ,w)

Отметим, что то же самое можно произвести, заменив горизонатальный угол обзора на вертикальный, но такой подход гораздо менее популярен.

Теперь специфика WebGL (а также — десктопных версий OpenGL): если холст/окно изменяет размер, нужно новый размер явно сообщить OpenGL при помощи метода viewport, иначе картинка будет продолжать рисоваться со старым размером.

Проще всего банально каждый кадр первым делом вызывать следующую функцию

function processResize() {
    const width = GL.canvas.clientWidth;
    const height = GL.canvas.clientHeight;
    const aspect = width / height;

    if (GL.canvas.height !== height || GL.canvas.width !== width) {
        GL.canvas.width = width;
        GL.canvas.height = height;
        GL.viewport(0, 0, width, height); 
    }

    return aspect;
}

Соответственно, полученное из неё соотношение сторон передавать в вершинный шейдер, в котором домножать на него y-координату.

Например, для рассматриваемого нами вращения куба функция рисования кадра (для fov в 90 градусов) примет вид

const renderFrame = time => {
    const aspect = processResize();

    GL.clearColor((1 + Math.cos(time/1000))/2, 0, 0, 1);
    GL.clear(GL.COLOR_BUFFER_BIT | GL.DEPTH_BUFFER_BIT);

    GL.useProgram(program);
    
    GL.bindVertexArray(cube);
    
    GL.uniform3f(uniforms.axis, 
        Math.cos(time/3000), 2*Math.cos(time/1700), 3
    );
    GL.uniform1f(uniforms.angle, time/1000);
    GL.uniform3f(uniforms.translation, 0, 0, 7);
    GL.uniform1f(uniforms.aspect, aspect);
    
    GL.drawArrays(GL.TRIANGLES, 0, 36);
    
    GL.bindVertexArray(null);

    requestAnimationFrame(renderFrame);
};

renderFrame(0);

А в вершинном шейдере должна появиться переменная uniform float aspect, использующаяся в строчке

gl_Position = vec4(position.x, position.y*aspect, -1, position.z);
// было gl_Position = vec4(position.xy, -1, position.z);

Также нужно не забыть добавить aspect в список названий uniform-переменных в функции setupScene.

Полезные функции GLSL

Кроме уже использованного выше normalize, в языке GLSL есть ещё несколько полезных функций. Перечислим некоторые из них.

Начнём с тригонометрии:

• sin, cos, tan — без комментариев
• asin, acos — вот этими функциями пользовать не нужно, потому что есть следующиая функция в двухаргументном варианте
• atan — предпочтительно пользоваться двухаргументной версией atan(y,x), которая возвращает угол, который вектор с координатами (x, y) составляет с положительным направлением первой оси; самое главное при её использовании — не перепутать порядок аргументов
• degrees, radians — функции для перевода радиан в градусы и обратно
• exp, log, exp2, log2 — натуральные и двоичные экспонента и логарифм

Продолжим геометрическими функциями:

• sqrt — квадратный корень
• inversesqrt — число, обратное квадратному корню
• length — длина вектора
• distance — расстояние между точками
• dot — скалярное произведение векторов
• cross — векторное произведение векторов
• normalize — масштабирует вектор так, чтобы его длина стала равной 1
• reflect — отражает первый аргумент относительно плоскости, перпендикуляром к которой является второй аргумент; второй аргумент нужно предварительно нормализовать

Закончим различными ступенчатыми функциями:

• abs, sign, floor, ceil, min, max — без комментариев
• mod — остаток от деления первого аргумента на второй
• fract — дробная часть (остаток от деления на 1)
• clamp — clamp(x,a,b) выдаёт a, если x<a; выдаёт b, если x>b; x, если x между a и b
• smoothstep — smoothstep(a,b,x) выдаёт 0, если x<a; выдаёт 1, если x>b; гладко интерполирует между 0 и 1, если x между a и b

Наиболее полезными, наверное, можно назвать dot и cross. Например, вышеприведённую функцию вращения можно переписать в терминах dot и cross следующим образом:

// t = t.z e12 - t.y e13 + t.x e23 + t.w e
vec4 lapply(vec4 t, vec3 v) {
    return vec4(t.w * v + cross(v, t.xyz), dot(v, t.xyz));
}

// v = v.x e1 + v.y e2 + v.z e3 + v.w e123
vec3 rapply(vec4 v, vec4 t) {
    return t.w * v.xyz - v.w * t.xyz + cross(t.xyz, v.xyz);
}

vec3 rotate(vec3 coord, vec3 axis, float angle) {
    axis = normalize(axis);
    float cosine_half = cos(angle / 2.0);
    float sine_half = sin(angle / 2.0);

    vec4 rot_r = vec4(sine_half * axis, cosine_half);
    vec4 rot_l = vec4(-rot_r.xyz, rot_r.w);

    return rapply(lapply(rot_l, coord), rot_r);
}

Такой простой вид достигается, как нетрудно видеть, засчёт использования для тензоров 2 ранга базиса \(e_{23}, -e_{13}, e_{12}\).

Также популярен базис, противоположный этому: \(I = -e_{23}\), \(J = e_{13}\), \(K = -e_{12}\). Тензоры \(I, J, K\) называются базисными кватернионами.

Дополнительно

Код с урока с медианами треугольника

Текстурирование и освещение

В прошлом разделе мы рассмотрели простейшую WebGL-программу, которая рисует вращающийся куб.

Его поверхность была разноцветной, но малореалистичной: на ней не хватало

• текстуры — рисунка деталей поверхности, заменяющего собой сложную высокодетализированную геометрию
• освещения, хотя бы примерно соответствующего тому, как освещены предметы в реальном мире

Начнём с небольшой модификации этой самой программы (если Вы не скомпоновали эту программу из кусков, приведённых в прошлом разделе, хотя бы один раз самостоятельно, рекомендуем сначала сделать это, а не копипастить нижеприведённый код)

let GL = null;

onload = () => {
    const canvas = document.getElementById(`CANVAS`);
    canvas.width = 600;
    canvas.height = 600;

    GL = canvas.getContext(`webgl2`);

    const { cube, program, uniforms } = setupScene();
    
    const renderFrame = time => {
        const aspect = processResize();

        GL.clearColor(0, 0, 0, 1);
        GL.clear(GL.COLOR_BUFFER_BIT | GL.DEPTH_BUFFER_BIT);

        GL.useProgram(program);
    
        GL.bindVertexArray(cube);
    
        GL.uniform3f(uniforms.axis, 
            Math.cos(time/3000), 2*Math.cos(time/1700), 3
        );
        GL.uniform1f(uniforms.angle, time/1000);
        GL.uniform3f(uniforms.translation, 0, 0, 7);
        GL.uniform1f(uniforms.aspect, aspect);
    
        GL.drawArrays(GL.TRIANGLES, 0, 36);
    
        GL.bindVertexArray(null);

        requestAnimationFrame(renderFrame);
    };

    renderFrame(0);
}


function processResize() {
    const width = GL.canvas.clientWidth;
    const height = GL.canvas.clientHeight;
    const aspect = width / height;

    if (GL.canvas.height !== height || GL.canvas.width !== width) {
        GL.canvas.width = width;
        GL.canvas.height = height;
        GL.viewport(0, 0, width, height); 
    }

    return aspect;
}


function setupScene() {
    const attributes = {
        coord: 0,
        index: 1,
    };

    const program = buildProgram(VS_SRC, FS_SRC, attributes);

    const cube = createCubeVAO(attributes);  

    GL.enable(GL.DEPTH_TEST);

    const uniforms = {};

    for (const name of ['axis', 'angle', 'translation', 'aspect']) {
        uniforms[name] = GL.getUniformLocation(program, name);
    }

    return { program, cube, uniforms };
}


function createCubeVAO(attributes) {
    const vao = GL.createVertexArray();

    GL.bindVertexArray(vao);

    const buffer = GL.createBuffer();

    GL.bindBuffer(GL.ARRAY_BUFFER, buffer);
    GL.bufferData(GL.ARRAY_BUFFER, makeCube(), GL.STATIC_DRAW);
   
    const { coord, index } = attributes;

    GL.enableVertexAttribArray(coord);
    GL.vertexAttribPointer(coord, 3, GL.FLOAT, false, 16, 0);

    GL.enableVertexAttribArray(index);
    GL.vertexAttribPointer(index, 1, GL.FLOAT, false, 16, 12);

    GL.bindVertexArray(null);

    return vao;
}


function compileShader(source, type) {
    let glType = type;

    if (type === 'vertex') { glType = GL.VERTEX_SHADER; }
    else if (type === 'fragment') { glType = GL.FRAGMENT_SHADER; }

    const shader = GL.createShader(glType);

    GL.shaderSource(shader, source);
    GL.compileShader(shader);


    if (!GL.getShaderParameter(shader, GL.COMPILE_STATUS)) { 
        console.error(`SHADER TYPE ${type}`);
        console.error(GL.getShaderInfoLog(shader));

        return null;
    }

    return shader;
}


function makeCube() {
    const v0 = [-1, -1, -1, 0];
    const v1 = [-1, -1,  1, 1];
    const v2 = [-1,  1, -1, 2];
    const v3 = [-1,  1,  1, 3];
    const v4 = [1,  -1, -1, 4];
    const v5 = [1,  -1,  1, 5];
    const v6 = [1,   1, -1, 6];
    const v7 = [1,   1,  1, 7];

    return Float32Array.from(
        v0.concat(v1).concat(v2)
        .concat(v1).concat(v2).concat(v3)
        .concat(v0).concat(v1).concat(v4)
        .concat(v1).concat(v4).concat(v5)
        .concat(v0).concat(v2).concat(v4)
        .concat(v2).concat(v4).concat(v6)
        .concat(v7).concat(v3).concat(v6)
        .concat(v3).concat(v6).concat(v2)
        .concat(v7).concat(v5).concat(v3)
        .concat(v5).concat(v3).concat(v1)
        .concat(v7).concat(v5).concat(v6)
        .concat(v5).concat(v6).concat(v4)
    ); 
}


function buildProgram(vsSource, fsSource, attributes) {
    const vs = compileShader(vsSource, 'vertex');
    if (vs === null) { return null; }

    const fs = compileShader(fsSource, 'fragment');
    if (fs === null) { return null; }

    const program = GL.createProgram();

    for (const name in attributes) {
        const index = attributes[name];

        GL.bindAttribLocation(program, index, name);
    }
    
    GL.attachShader(program, vs);
    GL.attachShader(program, fs);
    GL.linkProgram(program);

    if (!GL.getProgramParameter(program, GL.LINK_STATUS)) { 
        console.error(GL.getProgramInfoLog(program));

        return null;
    }

    return program;
}


const VS_SRC = `#version 300 es

in vec3 coord;
in float index;  // пока не убираем! (позже пригодится)

uniform vec3 axis;
uniform float angle;
uniform vec3 translation;
uniform float aspect;

// t = t.z e12 - t.y e13 + t.x e23 + t.w e
vec4 lapply(vec4 t, vec3 v) {
    return vec4(t.w * v + cross(v, t.xyz), dot(v, t.xyz));
}

// v = v.x e1 + v.y e2 + v.z e3 + v.w e123
vec3 rapply(vec4 v, vec4 t) {
    return t.w * v.xyz - v.w * t.xyz + cross(t.xyz, v.xyz);
}

vec3 rotate(vec3 coord, vec3 axis, float angle) {
    axis = normalize(axis);
    float cosine_half = cos(angle / 2.0);
    float sine_half = sin(angle / 2.0);

    vec4 rot_r = vec4(sine_half * axis, cosine_half);
    vec4 rot_l = vec4(-rot_r.xyz, rot_r.w);

    return rapply(lapply(rot_l, coord), rot_r);
}

void main() {
    float scale = 2.3;

    vec3 position = rotate(scale*coord, axis, angle) + translation;
    
    gl_Position = vec4(position.x, position.y*aspect, -1, position.z);
}
`;

const FS_SRC = `#version 300 es

precision highp float;

out vec4 frag_color;

void main() {
    frag_color = vec4(0.8, 0.5, 0.7, 1);
}
`;

Текстурирование

Для того, чтобы наложить рисунок на поверхность, нам потребуется этот самый рисунок.

В рамках браузера проще всего рисунки загрузить посредством img-элементов. Например, вставив в код страницы элемент вида

<img src="имя_файла" style="display:none" id="SOME_IMAGE">

Если лень искать картинку, можете воспользоваться кирпичами.

Общение с текстурами напоминает общение с буферами данных. А именно:

• нужно «создать» текстуру (методом createTexture)
• дать ей роль (методом bindTexture)
• перенести на неё изображение из оперативной памяти (методом texImage2D или texImage3D, в зависимости от роли текстуры)
• настроить её (методами texParameteri и texParameterf)
• если нужно, сгенерировать MIP-карты (методом generateMipmap)
• использовать в шейдере (при помощи uniform-переменной правильного типа)

Сейчас мы добавим в функцию настройки сцены следующий кусок:

const image = document.getElementById(`SOME_IMAGE`);
const texture = GL.createTexture();

GL.bindTexture(GL.TEXTURE_2D, texture);
GL.texImage2D(GL.TEXTURE_2D, 0, GL.RGBA, GL.RGBA, GL.UNSIGNED_BYTE, image);
GL.generateMipmap(GL.TEXTURE_2D);

В вершинный шейдер — новую выходную переменную

out vec2 tex_coords;

и в конце main вернём switch (только немного другой):

switch (int(index)) {
case 0:
    tex_coords = vec2(0, 0);
    break;
case 1:
    tex_coords = vec2(1, 0);
    break;
case 2:
    tex_coords = vec2(1, 0);
    break;
case 3:
    tex_coords = vec2(0, 0);
    break;
case 4:
    tex_coords = vec2(0, 1);
    break;
case 5:
    tex_coords = vec2(1, 1);
    break;
case 6:
    tex_coords = vec2(1, 1);
    break;
case 7:
    tex_coords = vec2(0, 1);
    break;
default:
    tex_coords = vec2(0, 0);
}

Во фрагментном же шейдере добавим две глобальные переменные:

in vec2 tex_coords;
uniform sampler2D tex;

и модифицируем main следующим образом:

void main() {
    frag_color = vec4(texture(tex, tex_coords).rgb, 1);
}

Опционально можно добавить в начало программы директиву

precision highp sampler2D;

которая может повысить качество отображения на некоторых мобильных устройствах.

Если теперь запустить то, что получилось, то мы увидим вращающийся куб, боковые стенки которого имеют на себе рисунок кирпича.

Внимание! Если Вы не видите вращающийся куб, загляните в консоль браузера. Если после исправления всех ошибок/опечаток Вы по прежнему ничего не видите, а бразуер ругается на origin изображения, откройте страницу не с локальной файловой системы, а запросом к веб-серверу. Проще всего в папке с файлами страницы запустить стандартный интерпретатор Python с опцией -m http.server. Это приведёт к поднятию на порту 8000 файлового сервера, выдающего файлы из той папки, из которой он был запущен. Соответственно, страницу можно открыть, введя в адресной строке браузера

http://127.0.0.1:8000/как_там_оно_называется.html

Если файл называется index.html, то можно и не указывать его имя: питоновский файловый сервер по умолчанию выдаёт именно его.

Что произошло?

Мы создали текстуру:

const texture = GL.createTexture();

Дали ей роль TEXTURE_2D:

GL.bindTexture(GL.TEXTURE_2D, texture);

Скопировали изображение в видеопамять:

GL.texImage2D(GL.TEXTURE_2D, 0, GL.RGBA, GL.RGBA, GL.UNSIGNED_BYTE, image);

После чего автоматически сгенерировали MIP-карты:

GL.generateMipmap(GL.TEXTURE_2D);

Для того, чтобы объяснить, что это такое, нужно пояснить, как вообще работают текстуры в OpenGL.

Во фрагментном шейдере мы воспользовались функцией texture, которая, получив на вход объект типа sampler2D и пару чисел, называемых текстурными координатами, выдала четырёхмерный вектор компонент цвета.

За то, как именно пикселям изображения сопоставляется этот вектор, отвечают в первую очередь следующие параметры:

• TEXTURE_MAG_FILTER
• TEXTURE_MIN_FILTER
• TEXTURE_WRAP_S
• TEXTURE_WRAP_T

которые можно настраивать методом texParameteri.

Текстурные координаты — пара действительных чисел (горизонтальная называется S, вертикальная называется T).

Первым делом они загоняются в рамки от 0 до 1: за то, как это происходит, отвечают параметры TEXTURE_WRAP_?. Возможные значения:

• REPEAT (значение по-умолчанию) — координата берётся по модулю единицы (то есть вычисляется остаток от деления координаты на 1)
• CLAMP_TO_EDGE — если координата меньше 0, она преобразуется в 0; если она больше 1, она преобразуется в 1
• MIRRORED_REPEAT — координата берётся по модулю двойки, значения от 1 до 2 меняют знак и далее берутся по модулю 1

Далее по полученной паре чисел, находящихся в пределах от 0 до 1, вычисляется точка на текстуре: пара нулей соответствует левому верхнему углу изображения, пара единиц — правому нижнему углу.

Также неким (вообще говоря, зависящим от используемой видеокарты; подробности см. в стандарте OpenGL) образом определяется режим интерполяции: минификация или магнификация.

Грубо говоря, минификация выбирается, если переход от пикселя рисуемого изображения к соседнему по хотя бы из одному направлений вызывает изменение текстурных координат, соответствующее смещению более чем на один пиксель текстуры. В противном случае выбирается магнификация.

В зависимости от того, какой из режимов был выбран, используется алгоритм, указанный в качестве значения параметра TEXTURE_MAG_FILTER (для магнификации) или же TEXTURE_MIN_FILTER (для минификации). Основных алгоритмов два:

• NEAREST — выбирается цвет того пикселя текстуры, куда попала точка, заданная текстурными координатами
• LINEAR (по умолчанию) — берётся взвешенная сумма цветов пикселей квадрата 2x2, центр которого находится ближе всего к точке, заданной текстурными координатами

При минификации могут полностью теряться некоторые детали изображения. Для того, чтобы уменьшить потери, используется технология MIP (от лат. multum in parvo — «много в малом»).

По изображению строятся MIP-уровни — последовательность текстур, каждая следующая из которых по обоим размерам в два раза меньше предыдущей (если какой-то из размеров стал равен 1, то во всех последующих изображениях он остаётся равным 1). Стандартный способ построения MIP-уровня — изображения разбивается на непересекающиеся квадраты 2x2, в каждом из которых цвет осредняется.

Если хочется воспользоваться MIP, нужно сгенерировать MIP-уровни. Это можно сделать как вручную при помощи texImage2D со вторым входом, отличным от нуля, так и автоматически — при помощи функции generateMipmap.

Для MIP доступно четыре возможных алгоритма минификации:

• NEAREST_MIPMAP_NEAREST — выбирается наиболее подходящий MIP-уровень, в рамках него применяется алгоритм NEAREST
• LINEAR_MIPMAP_NEAREST — выбирается наиболее подходящий MIP-уровень, в рамках него применяется алгоритм LINEAR
• NEAREST_MIPMAP_LINEAR (по умолчанию) — выбирается пара наиболее подходящих MIP-уровней, в каждом из них применяется алгоритм NEAREST, затем между полученными значениями происходит линейная интерполяция
• LINEAR_MIPMAP_LINEAR — выбирается пара наиболее подходящих MIP-уровней, в каждом из них применяется алгоритм LINEAR, затем между полученными значениями происходит линейная интерполяция; этот способ ещё называют трилинейной фильтрацией

В заключение ещё раз повторим основные этапы настройки текстуры:

• выбрать способ преобразования текстурных координат в диапазон от 0 до 1
• выбрать алгоритмы интерполяции значений при магнификации и минификации
• если при минификации используется MIP, нужно вызвать функцию generateMipmap

Также отметим, что больше всего на нарисованное изображение влияет магнификационный фильтр (при этом он не особо влияет на скорость рисования). Его следует выбирать, исходя исключительно из эстетических соображений.

А вот минификационный фильтр рекомендуется выбирать из MIP-вариантов: это всего лишь на треть увеличивает потребление памяти, но значительно повышает скорость рисования маленьких или далёких от глаза объектов. Почти единственное исключение: длинные объекты, направленные вдаль (например, дорога с разметкой, уходящая к горизонту). В этом случае правильно было бы использовать в направлении взгляда больший MIP-уровень (т.е. с меньшим разрешением), чем в направлении поперёк взгляда (это называется анизотропной фильтрацией), но такой режим работы поддерживают далеко не все устройства. В отсутствии же анизотропной фильтрации наиболее адекватное изображение в такой ситуации будут давать минификационные фильтры, не использующие MIP (потеря части деталей в направлении взгляда менее заметна, чем размытие в направлении поперёк взгляда).

Кривые пол и потолок куба

На нашем кубе две грани отображаются странно (выбранные нами текстурные координаты, очевидно, не подходят для этих граней). Вместо того, чтобы для каждой вершины каждого треугольника передавать именно её текстурные координаты, воспользуемся дешёвым трюком: изменим фрагментный шейдер на следующий

#version 300 es

precision highp float;
precision highp sampler2D;

out vec4 frag_color;

in float cube_x;
in vec2 tex_coords;

uniform sampler2D tex;

void main() {
    vec3 surface_color = 
        abs(cube_x) > 0.999
        ? vec3(0.7, 0.7, 0.7)
        : texture(tex, tex_coords).rgb;

    frag_color = vec4(surface_color, 1);
}

а в вершинный добавим глобальную переменную

out float cube_x;

которую внутри main сделаем равной coord.x.

Обратите внимание на > 0.999 вместо == 1.0. Последнее равенство, как ни странно, достигается лишь изредка, даже несмотря на то, что интерполяция производится между тремя единицами. Арифметика с плавающей точкой — странная вещь (и три числа, которые по идее должны давать в сумме единицу, не всегда её дают).

Рассеянный свет

Сейчас наш куб выглядит так, как будто она равномерно освещён со всех сторон: такое освещение называется фоновым (английский термин — ambient).

Достигается фоновое освещение банально умножением каждой компоненты цвета пикселя на какое-нибудь число.

Сейчас мы добавим к фоновому освещению рассеянное: его интенсивность в точке поверхности пропорциональна косинусу угла между нормалью к поверхности в этой точке и лучом, направленным от точки к источнику света.

Заодно мы введём в нашу программу вторую текстуру и воспользуемся ей как текстурой данных. А именно, при помощи неё мы передадим в программу массив всех источников освещения.

Начнём как раз с создания второй текстуры:

const lights = GL.createTexture();

GL.activeTexture(GL.TEXTURE1);
GL.bindTexture(GL.TEXTURE_2D, lights);
GL.texImage2D(GL.TEXTURE_2D, 0, GL.R32F, 4, 2, 0, GL.RED, GL.FLOAT, 
    Float32Array.from([
        4, 3, -5, 130,
        -4, 1, 3, 20,
    ])
);
GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MAG_FILTER, GL.NEAREST);
GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MIN_FILTER, GL.NEAREST);

Метод activeTexture выбирает текущую текстуру (с которой затем работают bindTexture, texImage2D, texParameteri и прочие подобные функции). Всего доступно не менее 32 текстур (с номерами от TEXTURE0 до TEXTURE31).

Далее мы записываем данные в память видеокарты, выбрав формат хранения R32F — в видеопамяти хранится только красная компонента 32-битным числом с плавающей точкой. Формат же данных в оперативной памяти задаётся парой RED/FLOAT (означает эта пара по сути то же, что и R32F).

Числа 4 и 2 — ширина и высота текстуры. В каждой строчке мы храним координаты источника света и его яркость.

Также, в отличие от рисунка поверхности, мы вынуждены переключить режимы минификации и магнификации на NEAREST: другие режимы текстурами формата R32F без MIP-карт не поддерживаются.

Модифицируем теперь вершинный шейдер, добавив в него

out vec3 position;

и убрав слово vec3 из соответствующей строчки функции main.

Фрагментный же шейдер приведём целиком, так как в нём много изменений:

#version 300 es

precision highp float;
precision highp sampler2D;  // обязательно!!!

out vec4 frag_color;

in float cube_x;
in vec3 position;
in vec2 tex_coords;

uniform sampler2D tex;
uniform sampler2D lights;

vec3 calculate_normal() {
    vec3 dir1 = dFdx(position);
    vec3 dir2 = dFdy(position);
    
    return normalize(cross(dir2, dir1));
}

void main() {
    vec3 surface_color = 
        abs(cube_x) > 0.999
        ? vec3(0.7, 0.7, 0.7)
        : texture(tex, tex_coords).rgb;

    float intensity = 0.3;  // фоновая интенсивность

    vec3 normal = calculate_normal();

    ivec2 lights_size = textureSize(lights, 0);

    for (int i = 0; i < lights_size.y; i++) {
        vec3 light_pos = vec3(
            texelFetch(lights, ivec2(0, i), 0).r,
            texelFetch(lights, ivec2(1, i), 0).r,
            texelFetch(lights, ivec2(2, i), 0).r
        );

        float light_intensity = texelFetch(lights, ivec2(3, i), 0).r;

        // направление от точки поверхности на источник света:
        vec3 direction = light_pos - position;
        float normal_direction = dot(normal, direction);

        if (normal_direction > 0.0) {
            float inv_distance = inversesqrt(dot(direction, direction));

            intensity += 
                light_intensity 
                * normal_direction
                * pow(inv_distance, 3.0);
        }
    }

    frag_color = vec4(intensity*surface_color, 1);
}

Прокомментируем некоторые его части:

• в нём появилась входная переменная in vec3 position — это в точности координаты рисуемого пикселя в пространстве
• также появилась вторая текстура uniform sampler2D lights — из управляющей программы нужно не забыть в этот uniform выставить номер текстуры, который у нас равен 1; в tex же по умолчанию выставлен 0 (но можно и явно его выставить — это не занимает много времени)
• функция calculate_normal вычисляет нормаль к поверхности в точке: она выбирает два независимых вектора, направленные в плоскости поверхности, вычисляя производные положения пикселя относительно экранных координат, затем считает их векторное произведение, автоматически получая вектор внешней нормали (если перемножить их в правильном порядке)
• наконец, основной цикл забирает из каждой текстуры соответствующие числа по их целочисленным координатам функцией texelFetch
• длина вектора direction пропорциональна расстоянию до источника света; соответственно, итоговая интенсивность источника обратно пропорциональна квадрату расстояния — это физически правильная, но не слишком реалистично выглядящая модель (поскольку в реальности в точку приходит ещё свет от того же источника, отражённый от близлежащих поверхностей)

Для получения работоспособной программы осталось не забыть получить из вершинной-фрагментной программы номер uniform-переменной lights и при рисовании кадра записать в эту переменную правильное значение командой

// обратите внимание на i
//                      |
//         /------------/
//         |
//         V
GL.uniform1i(uniforms.lights, 1);

Кроме точечных источников света часто рассматривают «направленные» — для них вектор направления света один и тот же для всех точек освещаемой поверхности.

В реальности примерно так работают всевозможные далёкие очень мощные источники света типа солнца, луны или же прожекторов.

В качестве полезного упражнения рекомендуем добавить в программу поддержку таких источников.

Массив текстур и нормальные карты

А сейчас мы продемонстрируем ещё один способ использования нескольких текстур — массив текстур. Все текстуры в массиве должны быть одного размера, зато их может быть весьма много (верхний предел обычно не менее 2048), и занимает массив ровно один номер текстуры (тот номер, который — вход activeTexture).

Заодно мы покажем такую технику, как карта нормалей. Карта нормалей — текстура, которая используется для построения нормалей к поверхности, отличных от нормали к треугольнику. Карты нормалей позволяют значительно повысить детализацию изображения, не усложняя его геометрию.

Для упрощения вычислений мы воспользуемся не полноценной картой нормалей, а картой высот. Предлагаем воспользоваться вот этой картинкой.

Сначала модифицируем наш код под использование массива текстур.

Первым делом нужно заменить в HTML-файле ссылку на изображение. Далее вместо

GL.bindTexture(GL.TEXTURE_2D, texture);
GL.texImage2D(GL.TEXTURE_2D, 0, GL.RGBA, GL.RGBA, GL.UNSIGNED_BYTE, image);
GL.generateMipmap(GL.TEXTURE_2D);

нужно написать

GL.bindTexture(GL.TEXTURE_2D_ARRAY, texture);
// здесь --vv стоит 3D вместо 2D
GL.texImage3D(GL.TEXTURE_2D_ARRAY,
    0, GL.RGBA, 
    image.width, image.height/2, 2, 0,
    GL.RGBA, GL.UNSIGNED_BYTE, image);
GL.generateMipmap(GL.TEXTURE_2D_ARRAY);

Наконец, в начало фрагментного шейдера нужно добавить строчку

precision highp sampler2DArray;

поменять тип переменной tex с sampler2D на sampler2DArray, а формулу

texture(tex, tex_coords).rgb

поменять на

texture(tex, vec3(tex_coords, 0)).rgb

после чего всё должно заработать в точности как и прежде.

Наконец, введём подсчёт нормали. Приведём здесь новую половину кода фрагментного шейдера:

#version 300 es

precision highp float;
precision highp sampler2D;
precision highp sampler2DArray;

out vec4 frag_color;

in float cube_x;
in vec3 position;
in vec2 tex_coords;

uniform sampler2DArray tex;
uniform sampler2D lights;

// далее мы добавим внешнее управление выраженностью выпуклостей:
uniform float bump;  

vec3 calculate_normal(bool top_bottom) {
    vec3 dir1 = dFdx(position);
    vec3 dir2 = dFdy(position);
    
    vec3 geometry_normal = normalize(cross(dir2, dir1));

    // чтобы не портило монотонно серые верх и низ
    if (top_bottom) { return geometry_normal; }

    // новая часть
    float dheight_dx = bump * dFdx(texture(tex, vec3(tex_coords, 1)).r);
    float dheight_dy = bump * dFdy(texture(tex, vec3(tex_coords, 1)).r);

    vec3 mdir1 = dir1 + geometry_normal * dheight_dx;
    vec3 mdir2 = dir2 + geometry_normal * dheight_dy;

    return normalize(cross(mdir2, mdir1));
}

void main() {
    bool top_bottom = abs(cube_x) > 0.999;

    vec3 surface_color = 
        top_bottom
        ? vec3(0.7, 0.7, 0.7)
        : texture(tex, vec3(tex_coords, 0)).rgb;

    float intensity = 0.3;  // фоновая интенсивность

    vec3 normal = calculate_normal(top_bottom);
 
    ... // ДАЛЕЕ ВСЁ БЕЗ ИЗМЕНЕНИЙ
}

Наконец, добавим на страницу слайдер:

<div><input id="BUMP_CONTROL" type="range" min="0" max="0.7" step="0.1"></div>

В onload добавим

const bumpControl = document.getElementById(`BUMP_CONTROL`);

а в функцию рисовния кадра

GL.uniform1f(uniforms.bump, parseFloat(bumpControl.value));

не забыв добавить bump в список имён uniform-переменных в функции setupScene.

Отражения и тени

Этот раздел посвящён кубическим текстурам.

Кубические текстуры представляют собой шестёрку изображений, цвета из которых получаются следующим образом:

• запрос к кубической текстуре осуществляется при помощи трёхмерного вектора
• луч, проведённый из нуля координат в направлении этого вектора, пересекается с кубом, центрированным в нуле координат и ориентированным по осям координат
• результирующий цвет получается таким, каким бы он был в соответствующей точке куба, если бы на грани этого куба были натянуты вышеупомянутые шесть изображений

Мы покажем два интересных применения кубических текстур:

• отражения (не очень точные, но неплохо выглядящие)
• тени (точные, но не очень качественные)

Программа-заготовка

Начнём со следующей программы:

let GL = null;

onload = () => {
    const canvas = document.getElementById(`CANVAS`);
    canvas.width = 600;
    canvas.height = 600;

    GL = canvas.getContext(`webgl2`);

    let angleX = 0;
    let tanY = 0;
    let angleY = 0;
    const camSpeed = 0.003;
    const camBoundY = 0.9;
    canvas.onclick = event => {
        canvas.requestPointerLock();
    };

    canvas.onmousemove = event => {
        if (document.pointerLockElement !== canvas) { return; }

        angleX += event.movementX*camSpeed;
        tanY -= event.movementY*camSpeed / camBoundY;
        if (tanY < -3) { tanY = -3; }
        else if (tanY > 3) { tanY = 3; }
        angleY = Math.atan(tanY) * camBoundY;
    };

    const { room, teapot } = setupScene();

    const renderFrame = time => {
        const aspect = processResize();

        GL.clearColor(0, 0, 0, 1);
        GL.clear(GL.COLOR_BUFFER_BIT | GL.DEPTH_BUFFER_BIT);

        const cameraPos = [
            2*Math.sin(angleX)*Math.cos(angleY), 
            2*Math.sin(angleY), 
            -2*Math.cos(angleX)*Math.cos(angleY)
        ];

        const teapotPos = [0.8*Math.sin(time/1300), 0, 0];

        room.begin();
    
        GL.uniform1f(room.uniforms.aspect, aspect);
        GL.uniform1f(room.uniforms.size, 3.5);
        GL.uniform3f(room.uniforms.camera_pos, ...cameraPos);
    
        room.draw();

        teapot.begin()
        
        GL.uniform1f(teapot.uniforms.aspect, aspect);
        GL.uniform1f(teapot.uniforms.size, 0.27);
        GL.uniform3f(teapot.uniforms.camera_pos, ...cameraPos);
        GL.uniform3f(teapot.uniforms.axis, 
            Math.cos(time/3000), 2*Math.cos(time/1700), 3
        );
        GL.uniform1f(teapot.uniforms.angle, time/1000);
        GL.uniform3f(teapot.uniforms.pos, ...teapotPos);
        
        teapot.draw();
    
        GL.bindVertexArray(null);

        requestAnimationFrame(renderFrame);
    };

    renderFrame(0);
}


function processResize() {
    const width = GL.canvas.clientWidth;
    const height = GL.canvas.clientHeight;
    const aspect = width / height;

    if (GL.canvas.height !== height || GL.canvas.width !== width) {
        GL.canvas.width = width;
        GL.canvas.height = height;
        GL.viewport(0, 0, width, height); 
    }

    return aspect;
}


function setupLights() {
    const lights = GL.createTexture();

    GL.bindTexture(GL.TEXTURE_2D, lights);
    GL.texImage2D(GL.TEXTURE_2D, 0, GL.R32F, 4, 2, 0, GL.RED, GL.FLOAT, 
        Float32Array.from([
            1, 1.5, -1, 7,
            -1, 1, 1, 5,
        ])
    );
    GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MAG_FILTER, GL.NEAREST);
    GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MIN_FILTER, GL.NEAREST);

    return lights;
}


function setupRoom(lights) {
    const attributes = {
        coord: 0,
        tex_coords: 1,
    };

    const {
        program,
        uniforms
    } = buildProgram(ROOM_VS, ROOM_FS, attributes, 
        ['camera_pos', 'aspect', 'size', 'tex', 'lights']
    );

    const vao = createCubeVAO(attributes);  

    const image = document.getElementById(`SOME_IMAGE`);
    const texture = GL.createTexture();

    const numImages = image.height / image.width;
    GL.bindTexture(GL.TEXTURE_2D_ARRAY, texture);
    GL.texImage3D(GL.TEXTURE_2D_ARRAY, 
        0, GL.RGBA, 
        image.width,
        image.width,
        numImages, 0,
        GL.RGBA, GL.UNSIGNED_BYTE, image);
    GL.generateMipmap(GL.TEXTURE_2D_ARRAY);


    const begin = () => {
        GL.useProgram(program);

        GL.activeTexture(GL.TEXTURE0);
        GL.bindTexture(GL.TEXTURE_2D_ARRAY, texture);

        GL.activeTexture(GL.TEXTURE1);
        GL.bindTexture(GL.TEXTURE_2D, lights);

        GL.bindVertexArray(vao);

        GL.uniform1i(uniforms.tex, 0);
        GL.uniform1i(uniforms.lights, 1);
    };

    const draw = () => {
        GL.drawArrays(GL.TRIANGLES, 0, 36);
    };

    return { uniforms, begin, draw };
}


function setupTeapot(lights) {
    const attributes = {
        coord: 0,
        normal: 1,
    };

    const {
        program,
        uniforms
    } = buildProgram(TEAPOT_VS, TEAPOT_FS, attributes, 
        ['camera_pos', 'aspect', 'size', 'pos', 'axis', 'angle', 'lights']
    );

    const vao = createTeapotVAO(attributes);  

    const begin = () => {
        GL.useProgram(program);

        GL.activeTexture(GL.TEXTURE0);
        GL.bindTexture(GL.TEXTURE_2D, lights);

        GL.bindVertexArray(vao);

        GL.uniform1i(uniforms.lights, 0);
    };

    const draw = () => {
        GL.drawArrays(GL.TRIANGLES, 0, TEAPOT_DATA.length / 6);
    };

    return { uniforms, begin, draw };
}


function setupScene() {
    GL.enable(GL.DEPTH_TEST);

    const lights = setupLights();

    return {
        room: setupRoom(lights),
        teapot: setupTeapot(lights),
    };
}


function createCubeVAO(attributes) {
    const vao = GL.createVertexArray();

    GL.bindVertexArray(vao);

    const buffer = GL.createBuffer();

    GL.bindBuffer(GL.ARRAY_BUFFER, buffer);
    GL.bufferData(GL.ARRAY_BUFFER, makeCube(), GL.STATIC_DRAW);
   
    const { coord, tex_coords } = attributes;

    GL.enableVertexAttribArray(coord);
    GL.vertexAttribPointer(coord, 3, GL.FLOAT, false, 24, 0);

    GL.enableVertexAttribArray(tex_coords);
    GL.vertexAttribPointer(tex_coords, 3, GL.FLOAT, false, 24, 12);

    GL.bindVertexArray(null);

    return vao;
}


function createTeapotVAO(attributes) {
    const vao = GL.createVertexArray();

    GL.bindVertexArray(vao);

    const buffer = GL.createBuffer();

    GL.bindBuffer(GL.ARRAY_BUFFER, buffer);
    GL.bufferData(
        GL.ARRAY_BUFFER, Float32Array.from(TEAPOT_DATA), GL.STATIC_DRAW
    );
   
    const { coord, normal } = attributes;

    GL.enableVertexAttribArray(coord);
    GL.vertexAttribPointer(coord, 3, GL.FLOAT, false, 24, 0);

    GL.enableVertexAttribArray(normal);
    GL.vertexAttribPointer(normal, 3, GL.FLOAT, false, 24, 12);

    GL.bindVertexArray(null);

    return vao;
}


function makeCube() {
    // геометрические координаты
    const v0 = [-1, -1, -1];
    const v1 = [-1, -1,  1];
    const v2 = [-1,  1, -1];
    const v3 = [-1,  1,  1];
    const v4 = [1,  -1, -1];
    const v5 = [1,  -1,  1];
    const v6 = [1,   1, -1];
    const v7 = [1,   1,  1];

    // текстурные координаты
    const t0 = [0, 0, 0];
    const t1 = [2, 0, 0];
    const t2 = [0, 2, 0];
    const t3 = [2, 2, 0];
    const t4 = [0, 0, 2];
    const t5 = [0, 2, 2];
    const t6 = [2, 0, 2];
    const t7 = [2, 2, 2];

    return Float32Array.from([]
        .concat(v0).concat(t4).concat(v1).concat(t5).concat(v2).concat(t6)
        .concat(v1).concat(t5).concat(v2).concat(t6).concat(v3).concat(t7) 
        .concat(v0).concat(t0).concat(v1).concat(t1).concat(v4).concat(t2)
        .concat(v1).concat(t1).concat(v4).concat(t2).concat(v5).concat(t3)
        .concat(v0).concat(t0).concat(v2).concat(t1).concat(v4).concat(t2)
        .concat(v2).concat(t1).concat(v4).concat(t2).concat(v6).concat(t3)
        .concat(v7).concat(t2).concat(v3).concat(t0).concat(v6).concat(t3)
        .concat(v3).concat(t0).concat(v6).concat(t3).concat(v2).concat(t1)
        .concat(v7).concat(t2).concat(v5).concat(t3).concat(v3).concat(t0)
        .concat(v5).concat(t3).concat(v3).concat(t0).concat(v1).concat(t1)
        .concat(v7).concat(t7).concat(v5).concat(t5).concat(v6).concat(t6)
        .concat(v5).concat(t5).concat(v6).concat(t6).concat(v4).concat(t4)
    ); 
}


function compileShader(source, type) {
    let glType = type;

    if (type === 'vertex') { glType = GL.VERTEX_SHADER; }
    else if (type === 'fragment') { glType = GL.FRAGMENT_SHADER; }

    const shader = GL.createShader(glType);

    GL.shaderSource(shader, source);
    GL.compileShader(shader);


    if (!GL.getShaderParameter(shader, GL.COMPILE_STATUS)) { 
        console.error(`SHADER TYPE ${type}`);
        console.error(GL.getShaderInfoLog(shader));

        return null;
    }

    return shader;
}


function buildProgram(vsSource, fsSource, attributes, uniformNames) {
    const vs = compileShader(vsSource, 'vertex');
    if (vs === null) { return null; }

    const fs = compileShader(fsSource, 'fragment');
    if (fs === null) { return null; }

    const program = GL.createProgram();

    for (const name in attributes) {
        const index = attributes[name];

        GL.bindAttribLocation(program, index, name);
    }
    
    GL.attachShader(program, vs);
    GL.attachShader(program, fs);
    GL.linkProgram(program);

    if (!GL.getProgramParameter(program, GL.LINK_STATUS)) { 
        console.error(GL.getProgramInfoLog(program));

        return null;
    }
    
    const uniforms = {};

    for (const name of uniformNames) {
        uniforms[name] = GL.getUniformLocation(program, name);
    }

    return { program, uniforms };
}



/*
Алгебра тензоров в базисе e23, -e13, e12, 
противоположном стандартному кватернионному.

Везде:

t = t.x e23 - t.y e13 + t.z e12 + t.w e
v = v.x e1 + v.y e2 + v.z e3 + v.w e123
*/
const TENSOR_ALGEBRA = `
vec4 tmul(vec4 t1, vec4 t2) {
    return vec4(
        t1.w * t2.xyz + t1.xyz * t2.w - cross(t1.xyz, t2.xyz),
        t1.w * t2.w - dot(t1.xyz, t2.xyz)
    );
}

vec4 lapply(vec4 t, vec3 v) {
    return vec4(t.w * v + cross(v, t.xyz), dot(v, t.xyz));
}

vec3 rapply(vec4 v, vec4 t) {
    return t.w * v.xyz - v.w * t.xyz + cross(t.xyz, v.xyz);
}

vec4 rotor(vec3 axis, float angle) {
    axis = normalize(axis);
    float cosine_half = cos(angle / 2.0);
    float sine_half = sin(angle / 2.0);

    return vec4(sine_half * axis, cosine_half);
}

vec3 rotate(vec4 t, vec3 v) {
    return rapply(lapply(vec4(-t.xyz, t.w), v), t);
}

vec3 rotate(vec3 coord, vec3 axis, float angle) {
    return rotate(rotor(axis, angle), coord);
}

vec3 apply_camera(vec3 v) {
    vec4 camera_rot = tmul(
        rotor(vec3(0, 1, 0), atan(camera_pos.x, -camera_pos.z)),
        rotor(vec3(1, 0, 0), atan(-camera_pos.y, length(camera_pos.xz)))
    );

    return rotate(camera_rot, v - camera_pos);
}
`;


const LIGHT_CALCULATION = `
float intensity = 0.3;

vec3 normal = calculate_normal();

ivec2 lights_size = textureSize(lights, 0);

for (int i = 0; i < lights_size.y; i++) {
    vec3 light_pos = vec3(
        texelFetch(lights, ivec2(0, i), 0).r,
        texelFetch(lights, ivec2(1, i), 0).r,
        texelFetch(lights, ivec2(2, i), 0).r
    );

    float light_intensity = texelFetch(lights, ivec2(3, i), 0).r;

    vec3 direction = light_pos - position;
    float normal_direction = dot(normal, direction);

    if (normal_direction > 0.0) {
        float inv_distance = inversesqrt(dot(direction, direction));

        intensity += 
            light_intensity 
            * normal_direction
            * pow(inv_distance, 3.0);
    }
}
`;


const ROOM_VS = `#version 300 es

in vec3 coord;
in float index;
in vec3 tex_coords;

out vec3 frag_tex_coords;
out vec3 position;

uniform float size;
uniform float aspect;
uniform vec3 camera_pos;

${TENSOR_ALGEBRA}

void main() {
    vec3 axis = vec3(0, 0, 1);
    float angle = radians(90.0);

    position = rotate(size*coord, axis, angle);

    vec3 cam_position = apply_camera(position);
    
    gl_Position = vec4(
        cam_position.x, cam_position.y*aspect, -0.1, cam_position.z
    );

    frag_tex_coords = tex_coords;
}
`;

const ROOM_FS = `#version 300 es

precision highp float;
precision highp sampler2D;
precision highp sampler2DArray;

out vec4 frag_color;

in vec3 position;
in vec3 frag_tex_coords;

uniform sampler2DArray tex;
uniform sampler2D lights;

vec3 calculate_normal() {
    vec3 dir1 = dFdx(position);
    vec3 dir2 = dFdy(position);
    
    vec3 geometry_normal = normalize(cross(dir2, dir1));

    float bump = 0.7;
    float dheight_dx = bump * dFdx(
        texture(tex, frag_tex_coords + vec3(0,0,1)).r
    );
    float dheight_dy = bump * dFdy(
        texture(tex, frag_tex_coords + vec3(0,0,1)).r
    );

    vec3 mdir1 = dir1 + geometry_normal * dheight_dx;
    vec3 mdir2 = dir2 + geometry_normal * dheight_dy;

    return normalize(cross(mdir2, mdir1));
}

void main() {
    vec3 surface_color = texture(tex, frag_tex_coords).rgb;

    ${LIGHT_CALCULATION}

    frag_color = vec4(intensity*surface_color, 1);
}
`;

const TEAPOT_VS = `#version 300 es

in vec3 coord;
in vec3 normal;

out vec3 position;
out vec3 frag_normal;

uniform float size;
uniform float aspect;
uniform vec3 pos;
uniform vec3 axis;
uniform float angle;
uniform vec3 camera_pos;

${TENSOR_ALGEBRA}

void main() {
    position = rotate(size*(coord - vec3(0,1.2,0)), axis, angle) + pos;
    frag_normal = rotate(normal, axis, angle);

    vec3 cam_position = apply_camera(position);
    
    gl_Position = vec4(
        cam_position.x, cam_position.y*aspect, -0.1, cam_position.z
    );
}
`;

const TEAPOT_FS = `#version 300 es

precision highp float;
precision highp sampler2D;

out vec4 frag_color;

in vec3 position;
in vec3 frag_normal;

uniform sampler2D lights;
uniform vec3 camera_pos;

vec3 calculate_normal() {
    return normalize(frag_normal);
}

void main() {
    vec3 surface_color = vec3(0.3, 0.6, 0.1);

    ${LIGHT_CALCULATION}

    frag_color = vec4(intensity*surface_color, 1);
}
`;

Для работы ей понадобится:

• текстура стен и пола комнаты — этот файл нужно вставить в HTML-страничку в img-элемент с идентификатором SOME_IMAGE
• трёхмерная геометрия чайника — этот файл нужно загрузить при помощи тега script

Эта программа несколько отличается от той, что предлагалось Вам сделать в прошлом разделе. Перечислим наиболее значимые отличия.

Камера

Первое, что бросается в глаза, — управление наблюдателем (или камерой, как этого наблюдателя традиционно называют), взгляд которого направлен в нуль координат.

Оно достигается засчёт uniform-переменной camera_pos, в которой хранится положение камеры.

Визуализация мира через камеру устроена весьма просто: произвести некоторые движения камеры — то же самое, что произвести движения мира, обратные им, в обратном порядке.

То есть, например,

• подвинуть камеру вперёд на 3 метра
• повернуть камеру направо на 30 градусов
• повернуть камеру вверх на 40 градусов

всё равно, что

• повернуть мир вниз на 40 градусов
• повернуть мир налево на 30 градусов
• подвинуть мир назад на 3 метра

Соответствующий набор действий производится в функции apply_camera всех вершинных шейдеров.

Чуть больше тензорной алгебры

Как можно заметить, функция apply_camera определена внутри некоторой общей для всех используемых нами вершинных шейдеров части, названной TENSOR_ALGEBRA.

В этой части функция поворота rotate разделена на две:

• генерирующую тензор поворота
• применяющую тензор поворота

Старая версия функции поворота тоже оставлена со старым же названием (GLSL поддерживает перегрузку функций), но теперь она выражена через новую функцию.

Также добавлено явное произведение тензоров смешанного 0 и 2 ранга, некоторые отголоски которого просматривались в lapply и rapply.

В настоящем примере оно излишне (хотя мы и показываем, как его можно использовать), но при более длинных композициях поворотов (и особенно — при анимации длинных сочленений, в которых каждое следующее звено повёрнуто относительно предыдущего) оно позволяет уменьшить общее количество вычислений.

Более прямолинейная процедура сборки шейдеров

Теперь не нужно после сборки программы запрашивать у этой программы номера uniform-переменных. Это делает сама функция сборки программы, возвращая в качестве результата работы не только программу, но и словарь индексов uniform-переменных.

Упрощённая процедура рисования

Теперь заключается в том, чтобы вызвать метод begin соответствующей части геометрии, выставить значения uniform-переменных и вызвать метод draw.

Сами методы begin и draw определены для каждого вида геометрии в соответствующей функции с названием вида setupТИП_ГЕОМЕТРИИ (конкретно setupRoom и setupTeapot).

У куба теперь есть полноценные пол и потолок

И этим всё сказано.

Изменена ближняя плоскость обрезания

Сейчас во всех вершинных шейдерах в качестве z-компоненты всех вершин стоит не -1, а -0.1. Соответственно, мы не видим лишь те точки, которые находятся на удалении, меньшем 0.1 от нас.

Визуализация зеркальной поверхности

Для визуализации отражений можно применять следующую методологию:

• всё окружение отражающего объекта рисуется с нескольких ракурсов так, чтобы эти ракурсы захватывали всевозможные направления
• нарисованное окружение записывается в кубическую текстуру
• при расчёте цвета пикселя отражающей поверхности выпускается луч из глаза наблюдателя, отражается от поверхности и результирующее направление запрашивается у кубической текстуры

Такой результат не слишком точен для точек поверхности, далёких от той, из которой делались рисунки окружения, но в том случае, когда отражающий объект достаточно мал по сравнению с размерами окружения, отражение получается довольно адекватным.

Буфер кадра

Для того, чтобы рисовать изображение не на холст, а в какую-нибудь текстуру, нужно создать т.н. буфер кадра:

const framebuffer = GL.createFramebuffer();
GL.bindFramebuffer(GL.FRAMEBUFFER, framebuffer);

// какая-то настройка

GL.bindFramebuffer(null);  // НЕ ЗАБЫВАТЬ!

Метод bindFramebuffer имеет двоякий эффект:

• инициализирует соответствующий буфер кадра
• выбирает этот буфер кадра в качестве того, на который рисуют методы наподобие drawArrays

Поэтому после настройки буфера кадра нужно не забыть снять с него выбор.

Есть очень важный момент: перед рисованием на буфере кадра необходимо выполнить метод viewport, в который передать размеры буфера кадра (выраженные в пикселях).

Ещё более важно не забыть опять вызвать viewport с размерами холста после снятия выбора с буфера кадра.

Для того, чтобы появилась возможность на буфер кадра рисовать, нужно прикрепить к нему текстуры, на которые будет сохраняться нарисованное изображение. Эти текстуры бывают двух видов:

• обычная двумерная или кубическая текстура (прикрепляется методом framebufferTexture2D)
• так называемый Renderbuffer — его нельзя использовать в качестве текстуры, но рисование на него более эффективно (прикрепляется методом framebufferRenderbuffer)

Соответственно, выбор между Renderbuffer и обычной текстурой довольно очевиден:

• ту часть картинки, которая нам понадобится в дальнейшем, нужно рисовать в обычную текстуру
• ту часть картинки, которая нужна только в процессе рисования на настоящий буфер кадра, нужно рисовать в Renderbuffer

В нашем случае отражений цвет окружения нам понадобится при рисовании отражающей поверхности, а вот массив глубин пикселей окружения нам совершенно бесполезен.

Соответственно, setupTeapot с учётом вышесказанного примет следующий вид:

function setupTeapot(lights) {
    const attributes = { coord: 0, normal: 1, };

    const {
        program,
        uniforms
    } = buildProgram(TEAPOT_VS, TEAPOT_FS, attributes, [
        'camera_pos', 'aspect', 'size', 'pos', 'axis', 'angle', 
        'lights', 'reflections'
    ]);

    const vao = createTeapotVAO(attributes);  
    
    const reflections = GL.createTexture();
    const resolution = 1024;

    GL.bindTexture(GL.TEXTURE_CUBE_MAP, reflections);
    GL.texStorage2D(GL.TEXTURE_CUBE_MAP, 1, GL.RGBA8, resolution, resolution);
    GL.texParameteri(GL.TEXTURE_CUBE_MAP, GL.TEXTURE_MIN_FILTER, GL.LINEAR);
    GL.texParameteri(GL.TEXTURE_CUBE_MAP, GL.TEXTURE_WRAP_S, GL.CLAMP_TO_EDGE);
    GL.texParameteri(GL.TEXTURE_CUBE_MAP, GL.TEXTURE_WRAP_T, GL.CLAMP_TO_EDGE);

    const framebuffer = GL.createFramebuffer();
    GL.bindFramebuffer(GL.FRAMEBUFFER, framebuffer);

    const depthbuffer = GL.createRenderbuffer();
    GL.bindRenderbuffer(GL.RENDERBUFFER, depthbuffer);
    GL.renderbufferStorage(
        GL.RENDERBUFFER, GL.DEPTH_COMPONENT24, resolution, resolution
    );
    GL.framebufferRenderbuffer(
        GL.FRAMEBUFFER, GL.DEPTH_ATTACHMENT, GL.RENDERBUFFER, depthbuffer
    );

    GL.bindFramebuffer(GL.FRAMEBUFFER, null);

    const begin = () => {
        GL.useProgram(program);

        GL.activeTexture(GL.TEXTURE0);
        GL.bindTexture(GL.TEXTURE_2D, lights);

        GL.activeTexture(GL.TEXTURE1);
        GL.bindTexture(GL.TEXTURE_CUBE_MAP, reflections);

        GL.bindVertexArray(vao);

        GL.uniform1i(uniforms.lights, 0);
        GL.uniform1i(uniforms.reflections, 1);
    };

    const draw = () => {
        GL.drawArrays(GL.TRIANGLES, 0, TEAPOT_DATA.length / 6);
    };

    return { uniforms, begin, draw, framebuffer, reflections, resolution };
}

Обратите внимание на следующее:

• настройки кубической текстуры — у нас нет MIP-уровней, поскольку мы перерисовываем текстуру каждый кадр, что влечёт необходимость нестандартного минификационного фильтра; также для кубических текстур настоятельно рекомендуется режим CLAMP_TO_EDGE по всем координатам (без него на рёбрах куба могут возникнуть артефакты)
• то, что пока мы не привязываем текстуру reflections к цветовой компоненте буфера кадра — это мы будем делать по 6 раз уже в процессе рисования сцены
• ОЧЕНЬ ВАЖНО! при рисовании в текстуру текстурные координаты \((0,0)\) окажутся у левого нижнего угла изображения. А используются текстуры обычно в предположении, что соответствующий угол левый верхний. Поэтому в большинстве случаев имеет смысл сразу рисовать в текстуру изображение, перевёрнутое по вертикали.

Ракурсы

Теперь нам нужно добавить возможность рисовать сцену в шести ракурсах:

• смотря вперёд
• смотря назад
• смотря вправо
• смотря влево
• смотря вверх
• смотря вниз

Добавим во все вершинные шейдеры новую переменную uniform int camera_dir (не забыв также её добавить в setup соответствующих объектов) и apply_camera заменим на

vec3 apply_camera(vec3 v) {
    vec4 camera_rot = camera_dir == 0 ? tmul(
        rotor(vec3(0, 1, 0), atan(camera_pos.x, -camera_pos.z)),
        rotor(vec3(1, 0, 0), atan(-camera_pos.y, length(camera_pos.xz)))
    ) : vec4(0,0,0,1);

    vec3 result = rotate(camera_rot, v - camera_pos);

    switch (camera_dir) {
    // Все ракурсы перевёрнуты по y!
    case 1:
        result.y = -result.y;
        break;
    case 2:
        result = -result;
        break;
    case 3:
        result = vec3(-result.zy, result.x);
        break;
    case 4:
        result = vec3(result.z, -result.yx);
        break;
    case 5:
        result.zy = result.yz;
        break;
    case 6:
        result.zy = -result.yz;
        break;
    }

    return result;
}

Если camera_dir отличен от 0, то камера будет направлена не к нулю координат, а в одном из вышеописанных шести направлений.

Также, из-за того, что теперь мы рисуем при camera_dir перевёрнутое изображение, необходимо модифицировать функцю calculate_normal фрагментного шейдера комнаты. А именно, её последнюю строчку заменить на

return normalize(camera_dir > 0
    ? cross(mdir1, mdir2)
    : cross(mdir2, mdir1)
);

добавив также в начало фрагментного шейдера декларацию

precision highp int;

и

uniform int camera_dir;

Теперь можно и нарисовать все 6 ракурсов. Для этого непосредственно перед кодом, рисующим чайник, вместо той части, которая рисует комнату, добавим вызов функции drawEnvironment, определённой так:

function drawEnvironment(room, teapot, aspect, cameraPos, teapotPos) {
    room.begin();
    
    GL.uniform1f(room.uniforms.aspect, aspect);
    GL.uniform1f(room.uniforms.size, 3.5);
    GL.uniform3f(room.uniforms.camera_pos, ...cameraPos);
    GL.uniform1i(room.uniforms.camera_dir, 0);
    
    room.draw();

    const directionToFace = {
        1: GL.TEXTURE_CUBE_MAP_POSITIVE_Z,
        2: GL.TEXTURE_CUBE_MAP_NEGATIVE_Z,
        3: GL.TEXTURE_CUBE_MAP_POSITIVE_X,
        4: GL.TEXTURE_CUBE_MAP_NEGATIVE_X,
        5: GL.TEXTURE_CUBE_MAP_POSITIVE_Y,
        6: GL.TEXTURE_CUBE_MAP_NEGATIVE_Y,
    };

    GL.bindFramebuffer(GL.FRAMEBUFFER, teapot.framebuffer);
    GL.viewport(0, 0, teapot.resolution, teapot.resolution);
    
    for (let i = 1; i <= 6; i++) {
        GL.uniform1f(room.uniforms.aspect, 1);  // тут единица!
        GL.uniform3f(room.uniforms.camera_pos, ...teapotPos);
        GL.uniform1i(room.uniforms.camera_dir, i);
        GL.framebufferTexture2D(GL.FRAMEBUFFER, GL.COLOR_ATTACHMENT0,
            directionToFace[i], teapot.reflections, 0);
        GL.clear(GL.COLOR_BUFFER_BIT | GL.DEPTH_BUFFER_BIT);
        room.draw();
    }

    GL.bindFramebuffer(GL.FRAMEBUFFER, null);
    GL.viewport(0, 0, GL.canvas.width, GL.canvas.height);
}

Осталось в процедуру рисования чайника не забыть дописать

GL.uniform1i(teapot.uniforms.camera_dir, 0);

Во фрагментном шейдере чайника дописать декларацию

precision highp samplerCube;

определить переменную

uniform samplerCube reflections;

и, наконец, модифицировать расчёт цвета пикселей поверхности чайника следующим образом:

float alpha = 0.3;
   
vec3 to_camera = camera_pos - position;
vec3 reflected = 2.0*dot(normal, to_camera)*normal - to_camera;
vec3 reflected_color = texture(reflections, reflected).rgb;

frag_color = vec4(
    alpha*intensity*surface_color + 
    (1.0-alpha)*reflected_color, 
1);

Число alpha отвечает за то, какую долю от цвета составляет рассеянный свет, а какую — отражённый.

Расчёт теней

Похожую технику можно применить для расчёта теней от источников освещения.

А именно, для каждого точечного источника можно нарисовать сцену в 6 ракурсах, центрированных в этом источнике, с тривиальным фрагментным шейдером. Наша задача — лишь заполнить глубинный буфер информацией о расстояниях от источника света до освещаемых им поверхностей.

Затем при рисовании итоговой картинки нужно по отдельности учесть каждый из этих источников света, а результирующие цвета правильно смешать.

Итого процедура рисования всей сцены приобретёт в нашем примере следующий вид:

• визуализируем комнату для отражений ровно так же, как и делали до этого, но пока не рисуем её на основной картинке
• для каждого источника света рисуем сцену в 6 ракурсах
• рисуем комнату и чайник с фоновым освещением и без отражений
• для каждого источника света: рисуем комнату и чайник с тенями от этого источника света
• наконец, рисуем частично прозрачные отражения на чайнике

Единственный кардинально новый момент во всём этом: смешение цветов, включаемое при помощи GL.enable(GL.BLEND) и обычно настраиваемое при помощи методов blendColor, blendEquation и blendFuncSeparate.

Смешение цветов

Для \(i\)-й компоненты пикселя её итоговое значение вычисляется по формуле:

цвет[i] = op(src[i]*f(src)[i], dst[i]*g(dst)[i])

где src — цвет только что нарисованного пикселя, dst — цвет пикселя на изображении, функции f и g задаются при помощи blendFuncSeparate, бинарная операция op задаётся при помощи blendEquation.

Возможных комбинаций функций f, g и op очень много. Здесь мы приведём лишь наиболее распространённые комбинации f и g в предположении, что op — сумма (значение по умолчанию).

Каждую комбинацию мы будем приводить как четвёрку входов для blendFuncSeparate:

• ONE, ZERO, ONE, ZERO — полная замена цвета пикселя (значение по умолчанию)
• ONE, ZERO, ZERO, ONE — замена цвета пикселя с сохранением старой альфа-компоненты
• SRC_ALPHA, ONE_MINUS_SRC_ALPHA, ZERO, ONE — альфа-компонента как непрозрачность (это — традиционная семантика альфа-компоненты)
• ONE, ONE, ZERO, ONE — аддитивное смешение цветов (аппроксимация смешения света от нескольких источников)
• DST_COLOR, ZERO, ZERO, ONE — мультипликативное смешение цветов (аппроксимация смешения нескольких красок)

Также обратим внимание на то, что при смешении цветов настоятельно рекомендуется переключить режим проверки глубины со стандартного «перерисовывать пиксель, если его глубина меньше сохранённой» на «перерисовывать пиксель, если его глубина не больше сохранённой» командой

GL.depthFunc(GL.LEQUAL);

Источники освещения, текстуры и шейдеры для них

Для начала модифицируем setupLights: для каждого источника света создадим отдельную текстуру, в которую будем записывать расстояния до точек сцены.

function setupLights(lightSources) {
    const lightsData = []; 
    const shadowmaps = [];
    const resolution = 1024;

    for (const source of lightSources) {
        lightsData.push(source.x, source.y, source.z, source.intensity);
        
        const shadowmap = GL.createTexture();
        GL.bindTexture(GL.TEXTURE_CUBE_MAP, shadowmap);
        GL.texStorage2D(GL.TEXTURE_CUBE_MAP, 1, GL.DEPTH_COMPONENT32F, resolution, resolution);
        GL.texParameteri(GL.TEXTURE_CUBE_MAP, GL.TEXTURE_MIN_FILTER, GL.NEAREST);
        GL.texParameteri(GL.TEXTURE_CUBE_MAP, GL.TEXTURE_MAG_FILTER, GL.NEAREST);
        GL.texParameteri(GL.TEXTURE_CUBE_MAP, GL.TEXTURE_WRAP_S, GL.CLAMP_TO_EDGE);
        GL.texParameteri(GL.TEXTURE_CUBE_MAP, GL.TEXTURE_WRAP_T, GL.CLAMP_TO_EDGE);

        shadowmaps.push(shadowmap);
    }


    const lightsTexture = GL.createTexture();

    GL.activeTexture(GL.TEXTURE1);
    GL.bindTexture(GL.TEXTURE_2D, lightsTexture);
    GL.texImage2D(GL.TEXTURE_2D, 0, GL.R32F, 4, lightSources.length, 0, GL.RED, GL.FLOAT, 
        Float32Array.from(lightsData)
    );
    GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MAG_FILTER, GL.NEAREST);
    GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MIN_FILTER, GL.NEAREST);

    
    const framebuffer = GL.createFramebuffer();

    return {
        sources: lightSources,
        dataTexture: lightsTexture,
        shadowmaps,
        resolution,
        framebuffer,
    };
}

Обратите внимание на DEPTH_COMPONENT32F в качестве внутреннего формата текстуры. Эта константа плохо документирована! Точнее, она отсутствует в документации к texImage2D и texStorage2D на MDN. В официальной документации к функции glTexStorage2D она присутствует.

Также обратите внимание на NEAREST-фильтры кубической карты расстояний: это — требование последнего пункта параграфа 3.8.13 стандарта OpenGL ES 3. Правда, оно, возможно, противоречит параграфу 3.8.8 (в котором слово «can» употребляется то ли в значении «может, но не обязан», то ли в значении «можно считать, что»), в результате чего при некоторых комбинациях ОС и браузера линейная фильтрация вполне работает (см. ответ от одного из разработчиков Firefox по ссылке).

Также модифицируем соответствующим образом setupScene:

function setupScene() {
    GL.enable(GL.DEPTH_TEST);

    const lightSources = [
        { x: 1, y: 1.5, z: -1, intensity: 7 },
        { x: -1, y: 1, z: 1, intensity: 5 },
    ];

    const lights = setupLights(lightSources);

    return {
        room: setupRoom(lights.dataTexture),
        teapot: setupTeapot(lights.dataTexture),
        lights,
    };
}

Затем напишем простой шейдер, единственное назначение которого — записать в компоненту глубины расстояние до точки (точнее, величину, обратно пропорциональную расстоянию, — в функции расчёта освещения уже есть величина такого рода, да и верхнего ограничения на расстояние у такой величины нет).

const SHADOWMAP_FS = `#version 300 es
precision highp float;

in vec3 position;

uniform vec3 camera_pos;

void main() {
    vec3 diff = position - camera_pos;

    gl_FragDepth = 1.0 - 0.1*inversesqrt(dot(diff, diff)); 
}
`;

От единицы мы её отнимаем, чтобы её можно было использовать как глубину при стандартной проверке глубины — при рисовании сцены относительно источников света проверка глубины, очевидно, требуется. Причём, в отличие от z-компоненты, для которой результат её деления на w-компоненту должен оказаться в пределах от -1 до 1, gl_FragDepth обязан быть от 0 до 1.

Теперь напишем функцию drawShadowmaps, которая рисует сцену с точки зрения каждого источника света в 6 ракурсах.

function drawShadowmaps(scene) {
    const {
        lights, room, teapot, teapotPos, teapotAxis, teapotAngle
    } = scene;

    GL.bindFramebuffer(GL.FRAMEBUFFER, lights.framebuffer);
    GL.viewport(0, 0, lights.resolution, lights.resolution);
  
    for (let i = 0; i < lights.sources.length; i++) {
        const light = lights.sources[i];
        const shadowmap = lights.shadowmaps[i];

        for (let dir = 1; dir <= 6; dir++) {
            GL.framebufferTexture2D(GL.FRAMEBUFFER, GL.DEPTH_ATTACHMENT,
                DIRECTION_TO_FACE[dir], shadowmap, 0);
            GL.clear(GL.DEPTH_BUFFER_BIT);

            room.beginShadow();
            GL.uniform3f(room.shadowUniforms.camera_pos, 
                light.x, light.y, light.z);
            GL.uniform1i(room.shadowUniforms.camera_dir, dir);
            room.draw();
            
            teapot.beginShadow();
            GL.uniform3f(teapot.shadowUniforms.camera_pos, 
                light.x, light.y, light.z);
            GL.uniform1i(teapot.shadowUniforms.camera_dir, dir);
            GL.uniform3f(teapot.shadowUniforms.axis, ...teapotAxis);
            GL.uniform1f(teapot.shadowUniforms.angle, teapotAngle);
            GL.uniform3f(teapot.shadowUniforms.pos, ...teapotPos);
            teapot.draw();
        }
    }

    GL.bindFramebuffer(GL.FRAMEBUFFER, null);
    GL.viewport(0, 0, GL.canvas.width, GL.canvas.height);
}

Общее для drawShadowmaps и drawEnvironment соответствие между номером ракурса и соответствующей OpenGL-константой, вынесем в глобальную переменную

let DIRECTION_TO_FACE = null; // это нужно вставить в начало

// это нужно вставить в соответствующее место onload:
DIRECTION_TO_FACE = {
    1: GL.TEXTURE_CUBE_MAP_POSITIVE_Z,
    2: GL.TEXTURE_CUBE_MAP_NEGATIVE_Z,
    3: GL.TEXTURE_CUBE_MAP_POSITIVE_X,
    4: GL.TEXTURE_CUBE_MAP_NEGATIVE_X,
    5: GL.TEXTURE_CUBE_MAP_POSITIVE_Y,
    6: GL.TEXTURE_CUBE_MAP_NEGATIVE_Y,
};

В функции drawShadowmaps используются методы room.beginShadow и teapot.beginShadow, которые мы реализуем, модифицировав соответствующим образом setupRoom и setupTeapot.

Приведём полный код для нового setupRoom, оставив setupTeapot в качестве упражнения для читателя

function setupRoom(lights) {
    const attributes = {
        coord: 0,
        tex_coords: 1,
    };

    const {
        program,
        uniforms
    } = buildProgram(ROOM_VS, ROOM_FS, attributes,
        ['camera_pos', 'camera_dir', 'aspect', 'size', 'tex', 'lights']
    );

    const {
        program: shadowProgram,
        uniforms: shadowUniforms,
    } = buildProgram(ROOM_VS, SHADOWMAP_FS, attributes, [
        'camera_pos', 'camera_dir', 'aspect', 'size',
    ]);

    const vao = createCubeVAO(attributes);  

    const image = document.getElementById(`SOME_IMAGE`);
    const texture = GL.createTexture();

    GL.bindTexture(GL.TEXTURE_2D_ARRAY, texture);
    GL.texImage3D(GL.TEXTURE_2D_ARRAY, 
        0, GL.RGBA, 
        image.width,
        image.height/4,
        4, 0,
        GL.RGBA, GL.UNSIGNED_BYTE, image);
    GL.generateMipmap(GL.TEXTURE_2D_ARRAY);


    const roomSize = 3.5;

    const begin = () => {
        GL.useProgram(program);

        GL.activeTexture(GL.TEXTURE0);
        GL.bindTexture(GL.TEXTURE_2D_ARRAY, texture);

        GL.activeTexture(GL.TEXTURE1);
        GL.bindTexture(GL.TEXTURE_2D, lights);

        GL.bindVertexArray(vao);

        GL.uniform1i(uniforms.tex, 0);
        GL.uniform1i(uniforms.lights, 1);
        GL.uniform1f(uniforms.size, roomSize);
    };


    const beginShadow = () => {
        GL.useProgram(shadowProgram);
        
        GL.bindVertexArray(vao);

        GL.uniform1f(shadowUniforms.aspect, 1);
        GL.uniform1f(shadowUniforms.size, roomSize);
    };


    const draw = () => {
        GL.drawArrays(GL.TRIANGLES, 0, 36);
    };

    return { 
        uniforms, shadowUniforms, begin, beginShadow, draw,
    };
}

Обратите внимание на то, что общий для двух программ размер комнаты мы вынесли в отдельную переменную и теперь выставляем в обеих begin-функциях. То же самое рекомендуем сделать и для чайника.

Наконец, реализуем шейдеры для освещения предмета одним источником:

const SINGLE_LIGHT_CALCULATION = `
float intensity = 0.3;

if (light.w > 0.0) {
    vec3 normal = calculate_normal();

    vec3 direction = light.xyz - position;
    
    float light_inv_distance = 10.0*(1.0 - texture(shadowmap, -direction).r);
    
    float normal_direction = dot(normal, direction);
    
    float inv_distance = inversesqrt(dot(direction, direction));

    if (normal_direction > 0.0 && inv_distance/light_inv_distance > 0.99) {
        intensity = 
            light.w
            * normal_direction
            * pow(inv_distance, 3.0);
    } else {
        intensity = 0.0;
    }
}
`;


const SINGLE_LIGHT_ROOM_FS = `#version 300 es
precision highp float;
precision highp sampler2DArray;
precision highp samplerCube;

out vec4 frag_color;

in vec3 position;
in vec3 frag_tex_coords;

uniform sampler2DArray tex;
uniform samplerCube shadowmap;

uniform vec4 light;

vec3 calculate_normal() {
    vec3 dir1 = dFdx(position);
    vec3 dir2 = dFdy(position);
    
    vec3 geometry_normal = normalize(cross(dir2, dir1));

    float bump = 0.7;
    float dheight_dx = bump * dFdx(
        texture(tex, frag_tex_coords + vec3(0,0,1)).r
    );
    float dheight_dy = bump * dFdy(
        texture(tex, frag_tex_coords + vec3(0,0,1)).r
    );

    vec3 mdir1 = dir1 + geometry_normal * dheight_dx;
    vec3 mdir2 = dir2 + geometry_normal * dheight_dy;

    return normalize(cross(mdir2, mdir1));
}

void main() {
    vec3 surface_color = texture(tex, frag_tex_coords).rgb;

    ${SINGLE_LIGHT_CALCULATION}

    frag_color = vec4(intensity*surface_color, 1);
}
`;


const SINGLE_LIGHT_TEAPOT_FS = `#version 300 es

precision highp float;
precision highp samplerCube;

out vec4 frag_color;

in vec3 position;
in vec3 frag_normal;

uniform samplerCube shadowmap;
uniform vec3 camera_pos;

uniform vec4 light;

vec3 calculate_normal() {
    return normalize(frag_normal);
}

void main() {
    vec3 surface_color = vec3(0.3, 0.6, 0.1);

    ${SINGLE_LIGHT_CALCULATION}
    
    frag_color = vec4(intensity*surface_color, 1);
}
`;

А основной шейдер для чайника поправим, добавив вход alpha и убрав оттуда освещение вообще:

const TEAPOT_FS = `#version 300 es

precision highp float;
precision highp samplerCube;

out vec4 frag_color;

in vec3 position;
in vec3 frag_normal;

uniform samplerCube reflections;
uniform vec3 camera_pos;
uniform float alpha;

vec3 calculate_normal() {
    return normalize(frag_normal);
}

void main() {
    vec3 normal = calculate_normal(); 

    vec3 to_camera = camera_pos - position;
    vec3 reflected = 2.0*dot(normal, to_camera)*normal - to_camera;
    vec3 reflected_color = texture(reflections, reflected).rgb;

    frag_color = vec4(reflected_color, alpha);
}
`;

В функции setupTeapot же модифицируем метод begin соответствующим образом:

const begin = () => {
    GL.useProgram(program);

    GL.activeTexture(GL.TEXTURE0);
    GL.bindTexture(GL.TEXTURE_CUBE_MAP, reflections);

    GL.bindVertexArray(vao);

    GL.uniform1i(uniforms.reflections, 0);
    GL.uniform1f(uniforms.alpha, 0.4);
    GL.uniform1f(uniforms.size, teapotSize);
}

Также добавим в setupRoom и setupTeapot сборку программы для освещения одним источником и метод beginSingleLight:

// для комнаты; для чайника напишите самостоятельно!
function setupRoom(lights) {
... // всё, как и прежде

    const {
        program: singleLightProgram,
        uniforms: singleLightUniforms,
    } = buildProgram(ROOM_VS, SINGLE_LIGHT_ROOM_FS, attributes, [
        'camera_pos', 'camera_dir', 'aspect', 'size', 'light', 'tex', 'shadowmap',
    ]);

... // всё, как и прежде
    
    const beginSingleLight = (light, shadowmap) => {
        GL.useProgram(singleLightProgram);

        GL.activeTexture(GL.TEXTURE0);
        GL.bindTexture(GL.TEXTURE_2D_ARRAY, texture);
        
        GL.activeTexture(GL.TEXTURE1);
        GL.bindTexture(GL.TEXTURE_CUBE_MAP, shadowmap);

        GL.bindVertexArray(vao);

        GL.uniform1i(singleLightUniforms.tex, 0);
        GL.uniform1i(singleLightUniforms.shadowmap, 1);
        GL.uniform1f(singleLightUniforms.size, roomSize);
        GL.uniform4f(singleLightUniforms.light, 
            light.x, light.y, light.z, light.intensity);
    };


... // всё, как и прежде

    return { 
        uniforms, shadowUniforms, begin, beginShadow, draw,
        singleLightUniforms, beginSingleLight, // два новых поля
    };
}

Теперь можно рисовать всю сцену (не забыв убрать из drawEnvironment первоначальное рисование комнаты):

const scene = {
    lights, room, teapot, aspect, 
    cameraPos, teapotPos, teapotAxis, teapotAngle
};

GL.blendFuncSeparate(GL.ONE, GL.ZERO, GL.ONE, GL.ZERO);
drawShadowmaps(scene);
drawEnvironment(scene);
drawObjects(scene);
drawReflections(scene);

Вот — новые определения вспомогательных функций (кроме drawShadowmaps, которая приведена выше):

function drawEnvironment(scene) {
    const { room, teapot, cameraPos, teapotPos } = scene;

    room.begin();

    GL.bindFramebuffer(GL.FRAMEBUFFER, teapot.framebuffer);
    GL.viewport(0, 0, teapot.resolution, teapot.resolution);
    
    for (let i = 1; i <= 6; i++) {
        GL.uniform1f(room.uniforms.aspect, 1);
        GL.uniform3f(room.uniforms.camera_pos, ...teapotPos);
        GL.uniform1i(room.uniforms.camera_dir, i);
        GL.framebufferTexture2D(GL.FRAMEBUFFER, GL.COLOR_ATTACHMENT0,
            DIRECTION_TO_FACE[i], teapot.reflections, 0);
        GL.clear(GL.COLOR_BUFFER_BIT | GL.DEPTH_BUFFER_BIT);
        room.draw();
    }

    GL.bindFramebuffer(GL.FRAMEBUFFER, null);
    GL.viewport(0, 0, GL.canvas.width, GL.canvas.height);
}

function drawObjects(scene) {
    const {
        lights, room, teapot, aspect, 
        cameraPos, teapotPos, teapotAxis, teapotAngle
    } = scene;

    for (let i = -1; i < lights.sources.length; i++) {
        if (i == 0) {
            GL.blendFuncSeparate(GL.ONE, GL.ONE, GL.ZERO, GL.ONE);
        }

        const light = i < 0
            ? { x: 0, y: 0, z: 0, intensity: 0 } 
            : lights.sources[i];

        const shadowmap = i < 0
            ? null 
            : lights.shadowmaps[i];

        room.beginSingleLight(light, shadowmap);
        GL.uniform1f(room.singleLightUniforms.aspect, aspect);
        GL.uniform3f(room.singleLightUniforms.camera_pos, ...cameraPos);
        GL.uniform1i(room.singleLightUniforms.camera_dir, 0);
        room.draw();
   
        teapot.beginSingleLight(light, shadowmap);
        GL.uniform1f(teapot.singleLightUniforms.aspect, aspect);
        GL.uniform3f(teapot.singleLightUniforms.camera_pos, ...cameraPos);
        GL.uniform1i(teapot.singleLightUniforms.camera_dir, 0);
        GL.uniform3f(teapot.singleLightUniforms.axis, ...teapotAxis);
        GL.uniform1f(teapot.singleLightUniforms.angle, teapotAngle);
        GL.uniform3f(teapot.singleLightUniforms.pos, ...teapotPos);
        teapot.draw();
    }

}


function drawReflections(scene) {
    GL.blendFuncSeparate(
        GL.SRC_ALPHA, GL.ONE_MINUS_SRC_ALPHA, GL.ZERO, GL.ONE
    );

    const { 
        teapot, teapotAxis, teapotAngle, teapotPos, aspect, cameraPos
    } = scene;
    
    teapot.begin();
        
    GL.uniform1f(teapot.uniforms.aspect, aspect);
    GL.uniform3f(teapot.uniforms.camera_pos, ...cameraPos);
    GL.uniform1i(teapot.uniforms.camera_dir, 0);
    GL.uniform3f(teapot.uniforms.axis, ...teapotAxis);
    GL.uniform1f(teapot.uniforms.angle, teapotAngle);
    GL.uniform3f(teapot.uniforms.pos, ...teapotPos);
        
    teapot.draw();
}

В setupScene включим cмешение цветов при помощи GL.enable(GL.BLEND) и переключим проверку глубины на GL.depthFunc(GL.LEQUAL), и всё готово!

Темы проектов

Этот раздел будет постепенно пополняться.

Во всех проектах, если не сказано иного, требуется реализовать какую-либо схему управления наблюдателем: либо хождение по поверхности, либо «свободную камеру», либо камеру с фиксированной точкой фокуса.

Фрактальная мельница

Пирамида. Из верхушки перпендикулярно высоте пирамиды идёт ось. На оси — вращающиеся лопасти (в количестве не менее 3 штук). На конце каждой лопасти — такая же пирамида с лопастями, только меньше. И так далее.

Должна быть возможность рисовать до четырёх уровней таких пирамид (общим числом не менее \(1+3+9+27=40\)).

Рекомендации:

• для каждого объекта хранить его ориентацию относительно того объекта, к которому он прикреплён
• ориентацию хранить либо матрицей (что несколько сложнее для отладки, но может требовать чуть-чуть меньше вычислений), либо кватернионом (тензором, составленным из \(e, e_{12}, e_{13}, e_{23}\)) и вектором сдвига

За текстуры, землю, небо, освещение и тени — отдельные бонусы. Также отдельный бонус за освоение drawArraysInstanced.

Бассейн

Комната. Половина пола на одном уровне, половина — на другом. В той части, которая ниже уровнем, налита вода, отражающая и преломляющая свет. На воде должна быть рябь. На стенах комнаты — какие-нибудь текстуры (например, стандартная керамическая плитка).

Рекомендации:

• рябь на воде не обязательно должна быть реалистичной; можно использовать, например, шум Перлина
• отражение и преломление можно реализовать визуализацией на пару текстур: при визуализации оба экрана можно расположить в плоскости воды, а камеру — недалеко под/над водой
• правильное направление отражённого/преломлённого луча можно отыскать тремя-четырьмя шагами бинарного поиска (постарайтесь обойтись без if) — см. иллюстрацию

За металлическую лестницу, спускающуюся в бассейн, и тени — отдельные бонусы.

Бинпоиск:

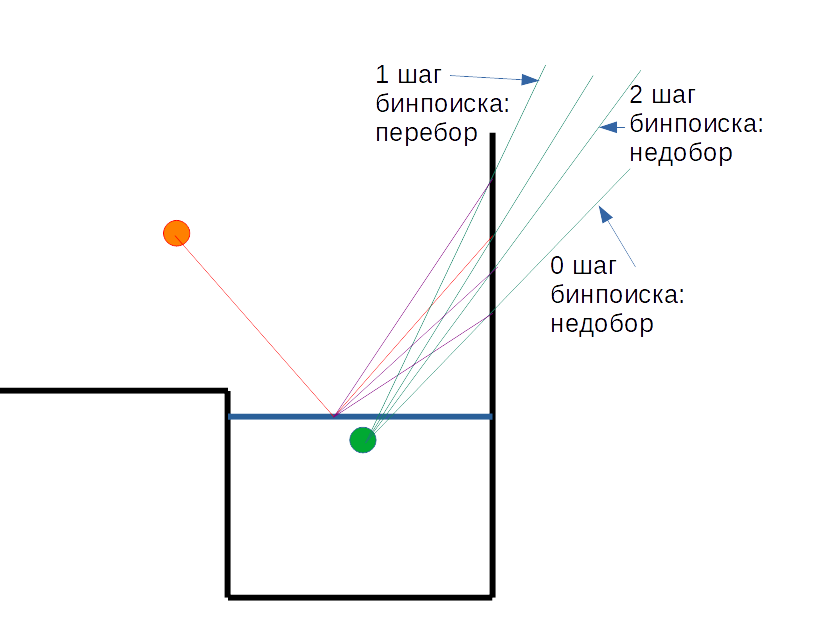
«Рекламный щит»

Рекламным щитом (billboard) называют плоское изображение, всегда обращённое к камере.

Требуется реализовать комнату, по которой летают несколько (не менее двух) идеальных сфер. Естественно, идеальную сферу нельзя собрать из треугольников. Зато можно визуализировать на плоской поверхности.

Соответственно, поверхности, на которых визуализируются сферы, должны быть всегда обращены к камере.

Рекомендации:

• в этом проекте эффектнее всего будет свободная камера, позволяющая переместиться в любую точку комнаты и выбрать произвольный ракурс
• траектории сфер стоит выбрать так, чтобы они не подлетали слишком близко друг к другу — потеряется весь эффект

За текстурирование и тени — отдельные бонусы.

Тени

Тут всего лишь требуется реализовать несколько предметов, летающих по комнате, и отбрасывающих тени.

Рекомендации:

• за основу можно взять программу, которую предлагалось реализовать в соответствующем разделе
• в качестве предметов можно взять просто кубы или что-нибудь настолько же примитивное

За текстурирование и визуализацию источников света техникой рекламных щитов или же каким-нибудь полноэкранным фильтром — отдельные бонусы.

Трассировка лучей

В точности то же, что и в прошлом проекте, но только тени нужно определять не при помощи теневых карт, а при помощи трассировки лучей: провести отрезок от освещаемой точки до источника света и проверить, не пересекается ли он с каким-либо из треугольников геометрии.

Также можно добавить примитивное глобальное освещение, учитывающее освещение не только источниками света напрямую, а светом, рассеянным и/или отражённым с других поверхностей.

Для этого достаточно выпустить из точки, цвет которой мы рассчитываем, несколько лучей в случайных направлениях (лучше их захардкодить, а не реализовывать в шейдерах генератор псевдослучайных чисел), а уже для пересечений этих лучей с геометрией рассчитать освещённость непосредственно источником света. Затем полученные освещённости, домноженные на косинусы соответствующих углов и делённые на вторую степень длин соответствующих отрезков, осреднить (сложить и поделить на количество лучей).

Рекомендации:

• не стоит использовать слишком сложную геометрию — достаточно пары кубов, летающих по комнате
• треугольники кубов можно передавать как в текстуре (но её придется каждый кадр изменять методом texSubImage2D), так и генерировать во фрагментном шейдере, передавая в него лишь положения кубов
• можно и положения кубов генерировать во фрагментном шейдере; но с текстурой координат треугольников итоговый код будет заметно проще

За текстурирование и визуализацию источников света — отдельные бонусы.

Комната с зеркалом

Комната, в которой на стене висит зеркало. Можно прямоугольной формы, а можно — и более интересной.

Ключевой момент — наблюдателя нужно визуализировать. Например, кубом с натянутой на него текстурой лица.

Также в комнате нужно расположить несколько предметов, которые можно увидеть из зеркала. Естественно, всё это должно быть освещено.

Рекомендации:

• проще всего банально нарисовать всю сцену два раза: одну — реальную и одну — мнимую, симметричную реальной относительно плоскости зеркала
• не забудьте отразить нормали в мнимой сцене
• также не забудьте отразить все источники света, освещающие зеркало
• как альтернатива, можно нарисовать сцену в текстуру с точки зрения «мнимого» наблюдателя, расположенного симметрично реальному относительно плоскости зеркала — такой подход может дать размытое изображение вблизи зеркала; также необходимо будет следить за тем, чтобы экран, на который рисуется сцена с точки зрения «мнимого» наблюдателя, соответствовал по форме таковому для реального наблюдателя

За реализацию бликов на зеркале от источника света, текстурирование, использующее нормальные карты, и участок комнаты, находящийся за зеркалом — отдельные бонусы.

Изометрический тетрис

Реализовать трёхмерную графику для какой-нибудь двумерной игры (например, тетриса, но можно выбрать и что-нибудь другое).

Рекомендации:

• игру нужно выбирать с простыми правилами — их нужно реализовать достаточно полноценно
• возможно, для некоторых игр более приятно будет выглядеть не центральная, а параллельная проекция
• отдельные объекты игры (например — кубики в тетрисе) должны быть визуально отличимы друг от друга (в том же тетрисе соседние кубики не должны сливаться в единый прямоугольник)

За реализацию управления мышкой (например, выделение фигур или клеток в шахматах или же — трёхмерных пунктов главного меню) — отдельный бонус. Также полагается бонус за возможность управления камерой.

Лабиринт

Реализовать достаточно большой лабиринт с возможностью перемещения по нему. Стены должны быть текстурированы, причём — несколькими различными текстурами.

Рекомендации:

• лабиринт можно как захардкодить, так и сгенерировать случайным образом
• придётся реализовать какой-нибудь формат хранения лабиринта
• можно, например, хранить только кубические блоки стен (как в Minecraft)
• или же можно хранить отрезки стен, совокуплённые с номером текстуры и коэффициентами, определяющими сдвиг и растяжение текстуры (как в Doom)

За реализацию дверей с возможностью их открывания/закрывания — отдельный бонус. Импорт первого уровня из Wolfenstein 3D также даёт отдельный бонус.

Меташары

Марширующие кубы. Это как квадраты, но только кубы.

Таблицы можно взять отсюда.

За расчёт поля нормалей к гладким (а не кусочно-треугольным) изоповерхностям — отдельный бонус. За освещение и тени — также отдельный бонус.